Задача по терверу

[Елена319]

Здравствуйте! Помогите, пожалуйста, с задачей!!Заранее огромное спасибо!!!!
Пусть случайные величины X1 и X2 независимы и распределены
по Пуассону (p(k,l1 ), p(k,l2 )). Доказать, что X1 +X 2 имеет
распределение Пуассона. Верно ли, что сумма двух независимых
случайных величин с геометрическим распределением также имеет
геометрическое распределение?
Еще раз спасибо!!!!!!!

[MaхVT]

Елена319 писал(а):

Пусть случайные величины X1 и X2 независимы и распределены
по Пуассону (p(k,l1 ), p(k,l2 )). Доказать, что X1 +X 2 имеет
распределение Пуассона.

Наверное, проще всего здесь воспользоваться аппаратом характеристических функций. А именно привлечь следующее утверждение: хар. функция суммы независимых случайных величин равна произведению хар. функций слагаемых.

Хар. функция распределения Пуассона с параметром $\lambda$ имеет вид $\varphi_{\pi_\lambda}(t)=e^{\lambda(e^{it}-1)}.$

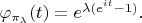
Если независимые величины $X_1$ и $X_2$ имеют распределение Пуассона с параметрами $l_1$ и $l_2$ соответственно, то хар. функция суммы $X_1+X_2$ равна

$$ \varphi_{X_1+X_2}(t)=\varphi_{X_1}(t)\varphi_{X_2}(t)=e^{{l_1} (e^{it}-1)}e^{{l_2}(e^{it}-1)}=e^{(l_1+l_2)(e^{it}-1)}. $$

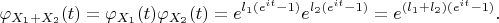
Для строгости осталось еще вспомнить теорему о том, что хар. функция случайной величины однозначно определяет её функцию распределения. Тогда мы можем сделать вывод, что величина $X_1+X_2$ распределена по Пуассону с параметром $l_1+l_2.$

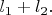
Аналогично решите задачу с геометрическим распределением.

[Елена319]

Спасибо Вам большое!!!!!

[PAV]

[mod="PAV"]Тема перемещена в карантин. Почему это произошло, можно понять, прочитав тему
Что такое карантин и что нужно делать, чтобы там оказаться
Там же описано, как исправлять ситуацию.[/mod]