Restricted perfect partitions

[Alik]

Здравствуйте, мне потребовалось отобрать подходящие к моему случаю ограниченные разбиения чисел (restricted partitions). Путем перебора и составления таблицы выяснилось, что подходящими являются некоторые замечательные разбиения (perfect partition). Чтобы подвести теорию под численный эксперимент пришлось покопаться в интернете и единственная статья с "живыми", красивыми примерами практически совпадающими с моим случаем это
Edwin O'Shea "M-partitions: Optimal partitions of weight for one scale pan"
Меня интересуют 4-х позиционные разбиения, приведенные на стр. 3 в Example 2.11. как Mp(8) и по Mp(15). Дело в том, что рассмотренные в статье разбиения обязательно включают единицу, в отличие от моих, которые приведены ниже и могут ее не содержать

Mp(8)
4     2     1     1
3     3     1     1
3     2     2     1

Mp(9)
5     2     1     1
4     3     1     1
4     2     2     1
3     3     2     1
3     2     2     2

Mp(10)
5     3     1     1
5     2     2     1
4     3     2     1

Mp(11)
6     3     1     1
6     2     2     1
5     3     2     1
4     4     2     1
4     3     3     1
4     3     2     2

Mp(12)
6     3     2     1
5     4     2     1

Mp(13)
7     3     2     1
6     4     2     1
4     4     3     2

Mp(14)
7     4     2     1
6     4     3     1

Mp(15)
8     4     2     1

Я не знаю как обобщить теорию, изложенную в статье на этот случай, несмотря на то, что имеется несколько статей на сходную тему. В частности немного из истории проблемы дается в Øystein J. Rødseth "Minimal r-Complete Partitions" в более ранней статье "Enumeration of M-partitions" этот же автор подсчитывает число таких разбиений

[maxal]

Alik в сообщении #179395 писал(а):

еня интересуют 4-х позиционные разбиения, приведенные на стр. 3 в Example 2.11. как Mp(8) и по Mp(15). Дело в том, что рассмотренные в статье разбиения обязательно включают единицу, в отличие от моих, которые приведены ниже и могут ее не содержать

Тогда надо сначала определить, что такое "мои разбиения". Приведенные в Example 2.11 разбиения являются всего лишь иллюстрацией строгого определения M-разбиений, данного в статье; и единицу они содержат не по прихоти автора, а потому, что это необходимое условие, которое следует из определения.
Если "ваши разбиения" могут не содержать единицы, то они не являются M-разбиениями, о которых идет речь в статьи. А, значит, и обсуждать их в контексте M-разбиений бессмысленно (по крайней мере пока вы не укажите их связь в явном виде).

[Alik]

maxal, чтобы объяснить как были получены мои разбиения я должен привести листинг программы в MATLAB. Проблема в том что она не дает формулу в явном виде, это всего лишь алгоритм проверки всех n-позиционных разбиений числа m на подходящие. Вкратце: имеется параметрическая система уравнений, программа подставляет каждое разбиение как параметр и смотрит решается система или нет. Поскольку c увеличением m число разбиений резко увеличивается, допустим P(63,4) = 1815, проверить все варианты крайне затруднительно. Анализируя свой алгоритм я нашел некоторые параллели с указанной статьей, поэтому и привожу ее в качестве reference, связь М-разбиений со своими в явном виде пока что не могу сформулировать. Более того, попрошу вашей помощи разобраться в статье Minimal r-Complete Partitions и выписать m-ary разбиения Mp(8) и по Mp(15), которые могут не содержать единицу, я хочу подставить их в программу и проверить.

[Alik]

Чтобы все таки ответить на вопрос maxal что такое "мои разбиения" нужно обратиться к последней странице топика http://dxdy.ru/topic11598-60.html
Приведенные разбиения подставляются в этот алгоритм в качестве вектора-маски $K$ и гарантированно дают решение каждой из систем уравнений.
Например после подстановки Mp(8) = 4 2 1 1 имеем 8 различных систем, для которых
{} & \begin{array}{c} x_1 = {4 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 9} \\ x_2 = {2\mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 9} \\ x_3 = {1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-\nulldelimiterspace} 9} \\ x_4 = {1 \mathord{\left/ {\vphantom {3 8}} \right. \kern-\nulldelimiterspace} 9} \\ \end{array} \\ \end{array} \\ \end{array}
В то время как $x_5$ принимает значения $1/9, 2/9, ..., 8/9$

[Alik]

Я очень надеюсь на участие людей разбирающихся в теории чисел, пока привожу свои соображения.
Из показанного примера ясно, что знаменатель это единица плюс сумма частей разбиения $9=1+8=1+ 4+2+1+1$. Таким образом, знаменатель подпадает под определение Completeness в статье "Minimal r-Complete Partitions", а именно $a_i=1+a_0+...+a_{i-1}$. Выпишем для случая $x_5=2/9$ все разбиения согласно алгоритму

     4     0    -1    -1
    -4    -2     0    -1
     4    -2     1    -1
     0     2     1    -1
    -4    -2    -1     0
     4    -2     0     0
     0     1     0     0
     4    -2    -1     1
     0     2    -1     1
     0     0     1     1

Очевидно, что знаменатель $9$ служит для дополнения отрицательных сумм до двух, в частности $2=9-7=9-4-2+0-1$. Отсюда можно сделать вывод, что если части разбиения Mp(8)=4 2 1 1 берутся со знаком, то Completeness сохраняется. Как это доказать для общего случая всех M-partitions я не знаю, но опять таки есть статья на эту тему:
George E. Andrews Euler's "De Partitio Numerorum"

[Alik]

Я, судя по нулевому количеству ответов, не сумел понятно сформулировать задачу, исправляюсь:
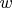
Let $w$ be the weight of M-partition $\lambda =(\lambda_0, \lambda_1, …, \lambda_n)$ of length $n+1$. According to the definition any number $m = 1 … w$ can be obtained uniquely as a sum of $\lambda_i$.
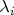
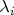
Permit the $\lambda_i$ to be positive, zero or negative, so that:
$k =a_0\lambda_0 + a_1\lambda_1 + … + a_n\lambda_n$
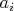
where $a_i$ takes just three values ${-1, 0, 1}$.
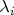
It is obvious that $k=m$ (runs over $1 … w$) at least once, when all $\lambda_i$ are positive, that is quite the M-partition. There is, however, a number of ways to obtain $k=m$ when the largest part $\lambda_n$ is positive. When $\lambda_n$ becomes negative, we have to examine the sub-partition $a_0\lambda_0 + a_1\lambda_1 + … + a_{n-1}\lambda_{n-1}$. If it is negative, $k$ is negative also and we replace $k$ by $w+k+1$. So, the negative values of $k$ are completed by $w+1$ that yields additional ways to obtain $k=m$.
Consider for example one of the M-partitions of $w=11$ written in the lexicographic order: $Mp(11)={4+4+2+1}$. The parts $\lambda = (4, 4, 2, 1)$ are used to represent $m=1$ and $m=2$ in the ways given below in the MATLAB format.

 [  12    -4    -4    -2    -1;
     0     4     0    -2    -1;
     0     0     4    -2    -1;
     0     4    -4     2    -1;
     0     0     0     2    -1;
     0    -4     4     2    -1;
     0     4    -4     0     1;
     0     0     0     0     1;
     0    -4     4     0     1 ]

[   12    -4    -4    -2     0;
     0     4     0    -2     0;
     0     0     4    -2     0;
     0     4    -4     2     0;
     0     0     0     2     0;
     0    -4     4     2     0  ]

The rank of first matrix is equal 5, while the rank of second matrix is 4. Designate the matrices of this type $A_m$ and the rank of $A_m$ by $rank(A_m)$.
So, the proposed conjectures for all $n+1$ length M-partitions are:
•$rank(A_m)\leqslant n+2$
•$rank(A_m)=n+2$ when $w+1$ is prime
•$rank(A_m)=n+2$ when $w+1$ is relatively prime to $m$