Monotonic sequence ?

[sasa]

If $a>0 \; ,\; x\in [0,1], $ and $ I_n(x):= n\int\limits_{0}^{1} t^{an-1}(1-x+xt)^n\; dt \; , $ prove

\[ \frac{1}{x+a}\le I_{n+1}(x)\le I_n(x) \le \frac{1-x+a}{a(1+a)} \; \; ,\; \; \; \forall n\in \{1,2,...\}, \]

and $ \displaystyle \lim\limits_{n\to \infty}I_n(x)=\displaystyle \frac{1}{x+a} $ uniformly on $[0,1] . $

[Руст]

Легко вычислить по частям интегралы:
$I_n(x)=\frac 1a \int_0^1 (1-x+xt)^ndt^{an}=\frac 1a -\frac{nx}{a(an+1)}+\frac{an(n-1)x^2}{a(an+1)(an+2)}-\dots+\frac{n!(-x)^n}{a(an+1)...(an+n)}$.
Отсюда легко получается, что предел равен 1/(a+x) и $I_n(x)>1/(a+x),I_1(x)=\frac{a+1-x}{a(a+1)}$.
Монотонность получается из разложения в ряд по (1-x) взяв интеграл переходя к переменной 1-t.

[Руст]

Монотонность кажется не всегда. Вот выкладки:
(1) $I_n(x,a)=(n+1)\int_0^1 t^{a(n+1)-1}(1-x+xt)^n[(1-x+xt]dt=\frac{(n+1)(1-x)}{n}I_n(x,\frac{a(n+1)}{a})+\frac{(n+1)x}{n} I_n(x,\frac{a(n+1)+}{n})$.
Учитывая, то что выражение монотонно убывает по а получаем двухсороннее неравенство:
(2) $\frac{n+1}{n}I_n(x,\frac{a(n+1)+1}{n})<I_{n+1}(x,a)<\frac{n+1}{n} I_n(x,\frac{a(n+1)+1}{n}).
Взяв интеграл для номера n+1 по частям получаем:
(3) $I_{n+1}(x,a)=\frac 1a -\frac{x(n+1)}{an}I_n(x,\frac{a(n+1)+1}{n}.
Подставив последнее в неравенства получаем:
(4) $\frac{1}{a+x+x/n}<I_n(x,a)<\frac{1}{a+x+(x-1)/n}.
Вместо правой границы можно получить так же неравенство:
(5) $I_n(x,a)<\frac{1}{a+x+(a-x)/(an+1)}.
Возможно при получении последнего я допустил ошибку в выкладках, иначе нарушается монотонность.

[Руст]

Подставляя (4) в (3) получается уточнение неравенства:
(5) $\frac{1}{a+x} \le I_n(x,a) \le \frac{1}{a+x-\frac{x(1-x)}{an+1-x}} $.
Причём неравенство сверху верна при n>1. Таким образом можно и далее уточнять вехнюю и нижнюю оценку. Однако при этом происходит сдвиг по n для которых оно справедливо и рациональные выражения всё более усложняются. Никакого противоречия с монотонностью (полученной из-за ошибки в выкладках) нет.

[sasa]

Цитата:

Three no-complete answers to the same question ?
...........................................?.........

My solution depends on "Bernstein polynomials".
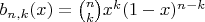
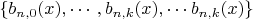
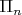
Denote $b_{n,k}(x)={n\choose k}x^k(1-x)^{n-k} $ and define $ f:[0,1]\to {\mathbb R} \; ,\; f(x)=\frac{1}{x+a} \; .$ Let us remind that in fact $ \left\{b_{n,0}(x),\cdots ,b_{n,k}(x), \cdots b_{n,k}(x)\right\} $ is the Bernstein basis of the vectorial space $\Pi_n $ of all (real) polynomials of degree $ \el n $ .
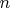
Remark: The polynomial

\[ \left(B_ng\right)(x):= \sum\limits_{k=0}^{n}b_{n,k}(x)g\left(\frac{k}{n}\right) \]

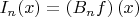
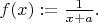
is known as Bernstein polynomial corresponding to a function $g:[0,1]\to {\mathbb R}. $ See (S.N.Bernstein, 1912, Harkov) Recognize that $I_n(x)= \left(B_nf\right)(x) $ where $f(x):=\frac{1}{x+a} $. Further we have

\[ (*)\; \; \; \; \; \; I_n(x)-I_{n+1}(x)= n(n+1)x(1-x)\sum\limits_{k=0}^{n-1}b_{n-1,k}(x)D_{k,n}[f] \]

where $ D_{k,n}[f]:=\alpha_k f\left(\frac{k}{n}\right)+\beta_kf\left(\frac{k+1}{n}\right) - f\left(\frac{k+1}{n+1}\right) $ with

\[\alpha_k:= \frac{k+1}{n+1}\; \; \; ,\; \; \; \beta_k:=\frac{n-k}{n+1}\; . \]

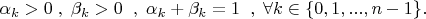
Observe that $ \alpha_k> 0 \; ,\; \beta_k>0 \; \; ,\; \alpha_k +\beta_k=1 \; \; ,\; \forall k\in \{0,1,...,n-1\} . $ Moreover

\[ \alpha_k\cdot \frac{k}{n}+\beta_k\cdot \frac{k+1}{n+1} =\frac{k+1}{n+1} \; . \]

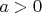
Because for $ a>0 $ the function $f:[0,1]\to {\mathbb R}$ is (strictly)- convex , we have $ D_{k,n}[f]>0 $ . In conclusion $ (*) $
show us that $I_n(x) \ge I_{n+1}(x) \; \; ,\; \; x \in [0,1] . $
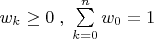
Now , if $w_k\ge 0 \; ,\; \sum\limits_{k=0}^{n}w_0=1 \; $ then according to Jensen inequality we have

\[ F\left(\sum\limits_{k=0}^{n}w_k\frac{k}{n}\right)\le \sum\limits_{k=0}^{n}w_kF\left(\frac{k}{n}\right) \]

for any convex function $F:[0,1]\to {\mathbb R} $ (convex on its domain).
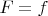
Select $ F=f $ and $ w_k=b_{n,k}(x)\; ,\; x\in [0,1].$ One finds

\[\begin{array}{c} \displaystyle f\left(\sum\limits_{k=0}^{n}b_{n,k}\frac{k}{n}\right)=f(x)=\frac{1}{x+a} \le \displaystyle \sum\limits_{k=0}^{n}w_kf\left(\frac{k}{n}\right)=\left(B_nf\right)(x) = I_n(x) \; . \end{array} \]

Note that in Russia there is a very good school regarding the topic " Bernstein polynomials": see
S.N.Bernstein (Commun.Soc.Math.Kharkow 13(1912) ),
E.Voronovskaja-1932 ,
L.V.Kantorovich -1930,1931,1934,
A.O.Gelfond -1950,
V.A. Baskakov -1960-1975,
Dzjadijh

P.P. Korovkin e.g. see : " Linear operators and approximation". Fizmatgiz, Moskow
1959, (also the translations: Delhi 1960 and Gordon and Breach, New York,
1960), MR 27 \# 561.
R.G. Mamedov -1959/1967,
N.A. Sapogov-1962/1964 ,
Yu.A. Saskin 1960-1970 ,
S.A. Teljakovskii -1965 ,
Timan ,
A.H. Tureckii -1961. ......

[Руст]

Я не понял, что улучшило применение многочленов Бернштейна?
То, что получается из (3) и (4) в моём изложении даёт в некотором смысле неулучшаумую границу сверху и снизу в виде (5) (при x=0 или x=1 вехняя граница совпадает с нижней и порядок стремления к нижней границе как простая функция от n так же неулучшаема). Причём можно получать и всё более усложнённые рациональные функции при наличии такой необходимости.