Да, конечно, я просто только недавно начал делать...ну, у меня последовательность выглядела таким образом

. Если она сходится к 1, тогда по определению получится

и соответственно для обратной

. Пусть
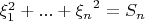
, тогда

и

. Если раскрыть модуль, то получится совокупность 2-х системм и вот на этом месте я пока остановился. По идее они ведь всегда должны выполняться...Если я это покажу, то и смогу доказать поставленую задачу. Идея вообще правильная?