Добавлю ещё, что термин "эквивалентность" применительно к вашему алгоритму явно неудачен. "Эквивалентность", даже если её понимать неформально, всё же предполагает некоторую транзитивность. А у Вас с этим может быть плохо.
Допустим, что

и

--- состояния первого автомата, а

и

--- состояния второго. Допустим, оба автомата приходят по слову

в состояния

и

, по слову

--- в состояния

и

, а по слову

--- в состояния

и

. Тогда

,

и

. Имея эти три "эквивалентности", логично было бы ожидать, что

. Однако я не вижу резонов, по которым должно было бы найтись слово, переводящее первый автомат в

, а второй --- в

.
Конечно, если состояния

и

имеют разные типы (конечное/не конечное), то исходные автоматы не эквивалентны, ибо, в связи с наличием слов

,

и

, тип состояния должен сохраняться вдоль всей цепочки

. Но всё же говорить про эквивалентность тут как-то неловко.
Я бы предпочёл всё излагать в терминах соответствий. Пусть

--- множество состояний первого автомата, а

--- множество состояний второго. Нас интересует соответствие

, такое что

Индуктивно

можно задать так:
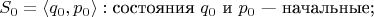


Легко показать, что для некоторого

справедливо

и

для этого

. Остаётся только найти требуемое

, что довольно просто сделать, пользуясь формулой перехода от

к

. Это произойдёт довольно быстро, так как справедлива оценка

.
На а далее всё просто: автоматы эквивалентны тогда и только тогда, когда состояния из любой пары, входящей в

, имеют один и тот же тип.
Программируется всё довольно легко. Если хотите, можете реализовывать этот, свой алгоритм. По сложности он такой же, как и мой, основанный на минимизации и сравнении двух минимальных автоматов.