я чесно так и не понял смысл комлпексных чисел, хоть и изучил их все, модет кто нибудь объяснить либо дать ссылку
Вот типичный пример, и вполне жизненный.
Берём колебательный контур, составленный из индуктивности

, с активным сопротивлением обмотки

и конденсатором

.
И интересуют нас процессы, которые там могут протекать. А протекают там (согласно теории дифуравнений) экспоненты типа

. Где

'ы определяются как корни характеристического уравнения:
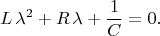
И если дискриминант положителен -- то все вроде и счастливы. Да только вот беда: наибольший практический интерес представляет как раз случай, когда сопротивление очень мало и, соотв., дискриминант отрицателен.
И что ж тут делать: сказать, что нет, мол, решений и в тую его, это уравнение?
Сказать-то можно, да только вот уравнение от этого никуда не исчезнет, а уж исходная задача -- и тем более.
Так что никуда не денешься: придётся придавать корням этого уравнения хоть какой-то смысл, а значит -- вводить комплексные числа.