Задача поставлена некорректно, так как импульс может быть приложен только с изменением граничных условий на конце.
Пусть

- скорость точек стержня

Начальные условия
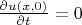
- в начальный момент времени ускорения равны нулю

- в начальный момент времени скорости везде равны нулю, кроме некоторой области вблизи конечной точки стержня.


Граничные условия

