Задачка на Чебышевский альтернанс

[Borat]

Добрый день!

Очень хотелось бы услышать подсказки к решению такой вот задачки: Доказать, что в случае, когда $f^{(n+1)}(x)$ сохраняет знак на $[a; b]$, чебышевский альтернанс содержит точки $a$ и $b$. Задача из Бахвалов, Жидков, Кобельков "Численные методы", глава 4, параграф 6, задача 5.

Заранее благодарен!

[Cave]

Borat
Вопользуйтесь много раз утверждением о том, что между любыми двумя нулями дифференцируемой функции лежит нуль ее производной.

[Borat]

Всё равно не очень понятно, что делать.

Пусть g(x) = f(x) - P_n(x)

У g(x) хотя бы n+1 нулей (т.к. точек альтернанса хотя бы n+2). Повторяя это много раз получаем, что

g^{(n)}(x) = f^{(n)}(x) - C

имеет хотя бы один нуль. Но т.к. эта функция монотонна, нулей ровно одна штука. Возвращаясь обратно получаем, что точек альтернанса должно быть ровно n+2. Но как получить, что крайние точки - границы сегмента приближения?

[Cave]

Borat
Сколько нулей может быть у функции $f'(x)$? У функции $f'(x) - P_n'(x)$? Чему они соответствуют в терминах альтернанса?

[Borat]

У разности - не менее n нулей

У f'(x) - неизвестно. Разве не так?

Добавлено спустя 33 минуты 47 секунд:

Лол, что-то я порядком тупил

Кажется, решение должно быть таким: пусть ни одна из граничных точек не будет точкой альтернанса. Это значит, что
$g(x) = f(x) - P_n(x)$
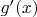
имеет по крайней мере $n + 2$ экстремума. Следовательно, $g'(x)$ имеет по крайней мере $n + 2$ нуля. Теперь (по уже упомянутой Cave) теореме Ролля это значит, что у $g''(x)$ как минимум n + 1 нуль. Повторяя это много раз получаем, что у $g^{(n+1)}(x) = f^{(n+1)}(x)$ должно быть по крайней мере 2 нуля, что противоречит условию. Чтобы избавиться от противоречия, "лишними" двумя точками альтернанса должны быть граничные точки сегмента (которые спокойно могут не быть экстремумами и не приносить нули производной).

Всем спасибо за моральную поддержку!

З.Ы. Почему теги math и значок $ ведут себя по-разному?

[Azog]

тег math обозначает начало кода в техе, а $, равно как и $$ это уже символы из теха, обозначающие начало/конец формулы. Если ничего не путаю то так =)

[Borat]

А, понятно, тут так настроено, что просто запись между

$...$

эквивалетна записи

[math]$...$[/math]

[Azog]

Прикольно. Не знал..

[Cave]

Borat
Всё так, но Чтобы избавиться от противоречия - это, во-первых, нездорово звучит и, во-вторых, этого мало (предположение было о том, что ни одна из концевых точек не принадлежит альтернансу - его отрицание заключается в том, что хотя бы одна принадлежит).
Да и вообще рассуждение от противного здесь, наверное, не нужно. $g^{(n+1)}(x) = f^{(n+1)}(x), поэтому у этой функции нет нулей, поэтому (применяя Ваше рассуждение) у $g'(x)$ не более $n$ нулей. Внутренние точки отрезка, принадлежащие альтернансу, являются нулями $g'(x)$, поэтому их не более $n$ штук, откуда всё и следует.