Асимптотика квазивогнутой плотности

[ZheniaM]

Уважаемые коллеги, нужна помощь в следующем вопросе.

Должна ли квазивогнутая плотность вероятности стремится к нулю при $x\to\infty$?
Сформулирую вопрос более чётко.

Имеется функция $f(x)$, удовлетворяющая следующим свойствам
1) $f(x)\geq 0$ для всех $x\in\mathds{R}^1$
2) $f(x)\in L_1[\mathds{R}^1]$
3) Для любых x,y\in A (где $A\subset\mathds{R}^1$ - выпуклое множество) и для любого $\lambda\in{[0,1]}$

$$ f(\lambda x+(1-\lambda)y)\geq\min\left\{f(x),f(y)\right\} $$

Должно ли выполняться $\lim\limits_{x\to\infty}f(x)=0?$

Скажем, если заменить условие 3 - просто условием вогнутости, то это утверждение верно. Оно скорее всего справедливо, если $f(x)$ логарифмически вогнута. Может быть надо будет потребовать некую гладкость или, скажем, непрерывность. Может быть кто-то сталкивался с утверждениями похожего типа?..

[Полосин]

Условие 3) поставлено нечетко. Что такое $A$? Если это некоторое заданное множество, отличное от $R$, то ответ отрицательный, поскольку в отдельных точках, не принадлежащих $A$, значения функции можно задавать произвольным образом. Если же условие 3) соблюдается для произвольного выпуклого $A$, то проще сразу писать "для любых $x, y \in R$". В этом случае ответ положительный. 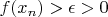Докажем от противного: пусть $x_n \rightarrow +\infty$, $f(x_n)>\epsilon>0$, тогда существуют точки $y_n\rightarrow +\infty$, в которых $f(y_n)<\epsilon $ (иначе функция не была бы интегрируемой на прямой), и в точках $x_n<y_m<x_{n+1}$ неравенство условия 3) нарушается.

[ZheniaM]

Спасибо за ответ!...Но вопрос уже не актуален.