Теорема Икланда и ее следствия

[zoo]

Вот решил разобраться с теоремой Икланда и некоторыми прилегающими вопросами. Сейчас напишу текст распечатаю и положу к себе в коллекцию. Все что написано ниже -- по материалам из интернета очень разного качества.

Пусть $X,d$ -- полное метрическое пространство.

Теорема (Ekland)

Пусть $\psi:X\to \mathbb{R}$ -- полунепрерывная сверху и ограниченная сверху функция.
Тогда для любого $\varepsilon>0$ существует $y\in X$ такой, что
$\psi(y)>\psi(x)-\varepsilon d(x,y)$
для всех $x\in X\backslash\{y\}.$
Кроме того $\psi(y)>\sup\psi(X)-\varepsilon$.




Доказательство.
Построим последовательность элементов $\{z^k\}\subset X $ и последовательность множеств
$S_k$ $k\in \mathbb{Z}_+$ следующим образом.

$z^0$ выберем из условия $\psi(z^0)>\sup\psi(X)-\varepsilon$ Такое $z^0$ существует в силу ограниченности сверху $\psi$.

Предположим, что $z^m$ известно и определим
$S_m=\{x\in X:\psi(z^m)\le \psi(x)-\varepsilon d(x,z^m)\}$

Выберем $z^{m+1}\in S_m$ так, что
$\psi(z^{m+1})\ge\sup\psi(S_m)-\frac{1}{m+1}$

Множества $S_m$ не пусты т.к. $z^m\in S_m$. Т.к. отображение
$\psi(\cdot)-\varepsilon d(\cdot,z^m) $полунепрерывно сверху, множества $S_m$ замкнуты.

Лемма 1. $S_{m+1}\subseteq S_m$.

Действительно, пусть $x\in S_{m+1}$
Тогда
$\psi(x)-\varepsilon d(x,z^m)\ge \psi(x)- \varepsilon d(x,z^{m+1})-\varepsilon d(z^{m+1},z^m)\ge \psi(z^{m+1})-\varepsilon d(z^{m+1},z^m)\ge \psi(z^m)$
ЧТД


Лемма 2 $\mathrm{diam}\, S_m\le \frac{2}{\varepsilon m}$

Доказательство.
Пусть $x\in S_m$ в силу леммы 1 $x\in S_{m-1}$.
Имеем $\varepsilon d(x,z^m)\le \psi(x)-\psi(z^m)\le \sup \psi(S_{m-1})-\psi(z^m)\le 1/m$
ЧТД

В силу леммы 2 последовательность $\{z^m\}$ является последовательностью Коши, предел этой последовательности обозначим через $y$, $z^m\to y$. По леммам 1, 2 и ввиду замкнутости множеств $S_m$ имеем $\{y\}=\bigcap_{k\in \mathbb{Z}_+}S_k$

Это и есть $y$ из формулировки теоремы. Предположим это не так. Т.е. найдется $x$, $x\ne y$ такой, что $\psi(x)-\varepsilon d(x,y)\ge\psi(y)$ Тогда
$\psi(x)-\varepsilon d(x,y)\ge\psi(y)\ge\psi(z^m)+\varepsilon d(y,z^m)$ для всех $m$.
Отсюда $\psi(x)\ge \psi(z^m)+\varepsilon (d(x,y)+d(y,z^m))\ge \psi(z^m)+\varepsilon d(x,z^m)$. Следовательно, $x\in \bigcap_{k\in \mathbb{Z}_+}S_k$ и $x=y$ Противоречие.
Теперь проверим второе неравенство теоремы. Для этого заметим, что $y\in S_0$ и поэтому
$\psi(y)>\psi(z^0)+\varepsilon d(z^0,y)>\sup\psi (X)-\varepsilon$.
Теорема доказана.

Теорема (Caristi)

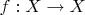
Предположим имеется отображене $f:X\to X$. И функция $\psi:X\to\mathbb{R}$ ограничена снизу и полунепрерывна снизу. Причем для всех $x\in X$ справедливо неравенство
$d(x,f(x))\le \psi(x)-\psi(f(x))$ Тогда отображение $f$ имеет неподвижную точку.

Доказательство.
В силу теоремы Икланда найдется $y$ такой, что $\psi(y)<\psi(x)+d(x,y)$ при всех $x\ne y$. Но из условия теоремы следует, что
$\psi(y)\ge d(y,f(y))+\psi(f(y))$ следовательно $f(y)=y$.
ЧТД

Если отображение $f$ -- сжимающее: $d(f(u),f(v))\le qd(u,v),\quad 0\le q<1$ то применяя только что доказаную теорему с функцией $\psi(x)=\frac{d(f(x),x)}{1-q}$ мы получим принцип сжатых отображений в части существования неподвижной точки.

Еще одна

Теорема (Caristi) (С небольшим моим уточнением)

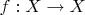
Предположим имеется отображене $f:X\to X$. И функция $\psi:X\to\mathbb{R}$ ограничена снизу и полунепрерывна снизу. Причем для всех $x\in X$ справедливо неравенство
$d(x,f(x))\le \psi(x)-\psi(f(x))$ Тогда если функция $\psi$ не достигает своего минимума на $X$ то множество неподвижных точек отображения $f$ некомпактно.

Доказательство. Пусть $W$ -- множество неподвижных точек $f$. По предыдущей теореме это множество не пусто. По теореме Икланда для любого $\varepsilon>0$ найдется $y\in X$ такой, что
$\varepsilon d(x,y)>\psi(y)-\psi(x)$ для всех $x$ таких что $x\ne y$. Как и выше, отсюда следует, что $y$ -- неподвижная точка $f$. Т.е. $y\in W$.

Предположим $W$ компактно. Тогда по условию теоремы $\inf \psi(X)<\min \psi(W)$ По теореме Икланда $\psi(y)<\inf\psi(X)+\varepsilon$ Выберем $\varepsilon$ так, что $\inf\psi(X)+\varepsilon<\min \psi(W)$. Таким образом $y\notin W$. Противоречие. ЧТД


Вот теперь можно идти преподуять.