функ ан:помогите решить задачу

[aerob]

подскажите как решить задачу:
Пусть $X, Y$ - линейные нормированные пространства. $A: X\rightarrow Y$ - ограниченный линейный оператор с $D(A)=X$, доказать, что

$$\|A\|= \sup_{x\in X, x\neq 0} \frac{\|Ax\|}{\|x\|}$$

.
(Треногин, Писаревский "Задачи и упражнения по ф...", 7.8)
объясните, что надо сделать чтобы указанное доказать
если норма оператора вводится по этому определению

$$\|A\|=\sup_{\|x\|\leqslant 1} \|Ax\|$$

,
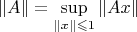
то понятно, что верхняя грань достигается при ||x|| = 1, а значит и в знаменателе будет 1 и равенство очевидно - это и есть доказательство?

[Alexey1]

Наверное необходимо сделать следующее

$$||A|| = \sup_{x \in X, x \neq 0} \frac {||Ax||} {||x||} = \sup_{x \in X, x \neq 0} ||A \frac x {||x||} || = \sup_{x \leqslant 1} ||A x ||$$

. Где использовалось условие, что вектор делённый на длину есть единичный вектор.

[ewert]

А вообще-то любопытная задачка -- доказать определение нормы оператора...

(нормальные люди считают

$$\|A\|=\sup_{\|x\|\leqslant 1} \|Ax\|$$

следствием определения)

[AD]

ewert писал(а):

(нормальные люди считают

$$\|A\|=\sup_{\|x\|\leqslant 1} \|Ax\|$$

следствием определения)

Представьте себе, я в прошлом году видел, как минимум, целый поток (~150 чел.) ненормальных людей. Включая меня.

[ewert]

Это просто в высшей степени неэстетично. Перед определением нормы должно идти определение ограниченности, типа $\Vert Ax\Vert\leqslant C\cdot\Vert x\Vert$. Тогда норма оператора совершенно естественным образом вводится как наилучшая из констант $C$ (или, что эквивалентно, как супремум отношения норм). При чём тут какие-то шары?...

[redhat]

похоже мы наблюдаем рождение конкурирующих школ функционального анализа