Доказать утверждение, наверное, можно следующим образом. Проверьте, пожалуйста.
1. Если найдется константа

, о которой идет речь в утверждении, то
![$\mathbb{E}[f(X)]\geq c\mathbb{E}[X]=0$ $\mathbb{E}[f(X)]\geq c\mathbb{E}[X]=0$](https://dxdy-02.korotkov.co.uk/f/5/9/7/5979df591d6ef171e5b97fff82f53f1082.png)
.
2. Пусть такой константы не существует. Определим

,

. В силу предположения,
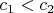
. Возьмем произвольное

. Найдутся числа

и

, такие, что

и

. Рассмотрим бинарную случайную величину

, принимающую значения

,

с вероятностями

и

, соответственно. Тогда
![$\mathbb{E}[X]=0$ $\mathbb{E}[X]=0$](https://dxdy-04.korotkov.co.uk/f/b/9/c/b9c8b26da611dff15acb53f1c60bc36b82.png)
, но
![$\mathbb{E}[f(X)]=f(x_1)\frac{x_2} {(x_2-x_1)}+f(x_2)\frac{-x_1} {(x_2-x_1)}<c'x_1\frac{x_2} {(x_2-x_1)}+c'x_2\frac{-x_1} {(x_2-x_1)}=0$ $\mathbb{E}[f(X)]=f(x_1)\frac{x_2} {(x_2-x_1)}+f(x_2)\frac{-x_1} {(x_2-x_1)}<c'x_1\frac{x_2} {(x_2-x_1)}+c'x_2\frac{-x_1} {(x_2-x_1)}=0$](https://dxdy-02.korotkov.co.uk/f/1/a/2/1a25e2729784d51835f481c488675ecc82.png)
.