Если бы

, то задача была бы простой: по главной диагонали стоят

- единички, ниже нее -

- нули, поэтому определитель равен 1. Поэтому удобно свести исходную задачу с

к задаче с

. Обозначим

. Как уже заметили,


- строка определителя с номером i является линейной комбинацией строк с номерами от 1 до i и строки решений в числах из

(а не из

). Складывая нужным образом строки мы получим для

строки из чисел решений в натуральных числах. И еще

. Тогда получаем,
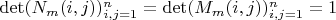
.