Функциональное уравнение с производной

[id]

Есть функциональное уравнение: найти все дифференциируемые $f: \mathbb{R} \to \mathbb{R}$, удовлетворяющие условию $f'(x) + xf(-x) = 1$.

Ответ мне неизвестен, но, полагаю, он не слишком страшный.
Ход моего решения:

$f'(x) = 1 - xf(-x)$.
Дифференциирую:
$f''(x) = -f(-x) + xf'(-x)$
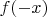
Подставляю значения для $f(-x)$ и $f'(-x)$ из первого тождества:
$f''(x) = \frac {f'(x) - 1} {x} + x(1 + xf(x))$
Т.е. $\forall x \neq 0$ имеет место о.д.у.
$xf''(x) = f'(x) - 1 + x^2 + x^3f(x)$

И вот тут встречается неприятность - так с ходу этот д.у. у меня решить не получается, а Maple 8 выдает монстроподобный ответ ( которого быть, наверно, не должно - задачка, кажется, олимпиадная ).

Что делать?

[redhat]

разложите функцию в сумму четной и нечетной , получите систему обыкновенных дифуров

$f(x)=u(x)+v(x)$ $u$ -чет ;$v$--неч

$u'(x)=-xu(x)$
$v'(x)=1+xv(x)$

[id]

redhat
Действительно, спасибо!
Так осталось решить только один нехороший диффур $v'(x)=1+xv(x)$

[Brukvalub]

id в сообщении #151753 писал(а):

Так осталось решить только один нехороший диффур $v'(x)=1+xv(x)$

Решайте его как линейное д.у.

[id]

Brukvalub
Но коэффициенты переменные, частное решение ( чтобы применить Остроградского-Лиувилля ) пока не вижу, но это, ясно, не многочлен.

Maple вот такое выдает:
$({\frac \pi 2}^{\frac 1 2} erf(2^{-\frac 1 2}x)+C_1)*exp({\frac {x^2} 2})$

[Brukvalub]

См. http://www.baurum.ru/differential-equalizations/8697/

[id]

Brukvalub
Разобрался, спасибо!

[Mikhail Sokolov]

Подставив в уравнении вместо $x$ переменную $-x$, получим еще одно уравнение. Вычитая второе уравнение из первого и вводя функцию $g(x)=f(x)+f(-x)$, получим: $g'(x)+xg(x)=0$. Решим это дифференциальное уравнение. Подставив решение в первоначальное уравнение, получим дифференциальное уравнение относительно $f$: $f'(x)+x(g(x)-f(x))=1$...

[mkot]

Цитата:

и вводя функцию $g(x)=f(x)+f(-x)$

Примечательно, что такая замена почти ничем не отличается от предыдущего решения, где
функция раскладывалась на чётную и нечётную составляющие, так как

$$\mathrm{even}(f(x)) = \frac{f(x) + f(-x)}{2},$$

$$\mathrm{odd}(f(x)) = \frac{f(x) - f(-x)}{2}.$$

[Mikhail Sokolov]

mkot Действительно, вы правы.

[Профессор Снэйп]

id писал(а):

Есть функциональное уравнение: найти все дифференциируемые $f: \mathbb{R} \to \mathbb{R}$, удовлетворяющие условию $f'(x) + xf(-x) = 1$.

Кстати, а какой физический смысл у этого диффура? Может ли такое уравнение возникнуть при описании какого-нибудь реального физического процесса?