Я так понимаю LQ равнозначно LU-разложению, правильно?
Поискал, скачал учебник...теперь вот сижу, изучаю))
Нет. Это разные вещи.

- разложение в произведение нижне-(

) и верхнетреугольной (

) матрицы.

- на нижнетреугольную(

) и ортогональную(

) матрицы. Скорее
всего по сути это Грам-Шмидт. Но выполняется разложение, конечно, не так, поскольку прямая ортогонализация неустойчива.
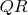
разложение обычно делается
преобразованиями Хаусхолдера или вращшениями Гивенса, впрочем все это сильно зависит
от типа матрицы (но копать скорее всего следует в этих направлениях). Вообще-то, на мой
взгляд, лучшая рекомендация в подобных случаях прежде всего заглянуть в Дж. Голуб, Ч. Ван Лоун "Матричные вычисления" (Matrix computations). Если это какой-то распространенный метод - там должно быть (тороплюсь - лень смотреть). Книга доступна в интернете, на английском - совсем легко найдете, на русском чуть придется поискать.