lihonosov писал(а):
Почему у Вас получилось 0,26
Ну во-первых у меня получилось

. Во-вторых примерно

, потому что ячейки с
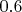
в таблице нет, и наилучшее приближение есть

.

- это то, что внутри таблицы (то что дано)

- это по краям (то что ищете)
Посмотрите хорошенько на график в методичке. Всё просто, например,

не может быть больше единицы.