matematikFromMati писал(а):
f(x) - диффереренцируема и неограничена на (a,b),
докакзать что g(x) неограничена на (a,b),
(g(x) - производная f(x))
От противного: если

ограничена на

, то есть, существует такое число

, что
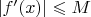
для всех
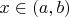
, то по теореме Лагранжа для любых различных

найдётся такая точка

(и даже лежащая между

и

), что

.