Помогите найти решение геометрической задачи (трапеция)

[gris]

Нестрого - точка В "движется от начала координат по направлению вдоль вектора DC".

Я рассматриваю четырехугольники в школьном понимании, то есть как замкнутые и несамопересекающиеся ломаные. Углы BAD и CDA предполагаются внутренними углами четырехугольника. Тогда из условия их суммы в 180 градусов следует параллельность AB и CD. То есть мы вообще-то ведем речь о трапециях и параллелограммах.

Вообще наши упражнения не имет особого смысла. В первоначальной постановке задачи речь шла о доказательстве теоремы. И достаточно всего лишь одного примера четырехугольника, не являющегося параллелограммом и удовлетворяющего её условиям , чтобы теорема опровергнуть.

Решения и их количество имеет смысл обсуждать, когда будет сформулированна задача. Например: сколько существует выпуклых четырехугольников с условиями задачи плюс заданные параметры: длина сторон, углы, размер отрезков. Может быть другие или только некоторые из этих. Да надо уточнить, являются ли углы BAD и CDA внутренними углами либо не обязательно. Рассматриваем ли мы невыпуклые и самопересекающиеся ломаные. Хорошо еще, что параллельнось AE И CF влечет двумерность четырехугольника. А то пришлось бы рассматривать его в трехмерном пространстве.

Интуитивно всем было понятно, что Вы понимаете под количеством решений. Мой ответ - 2 или 1. А если разговаривать серьезно, то нужна четко сформулированная постановка задачи.

[VAL]

TOTAL писал(а):

VAL писал(а):

Вполне может. И даже четыре может.
Я фиксировал точки A,B,C,E и вращал AD вокруг A

А я не вращал.

Ну и зря!

Цитата:

Но если разрешается делать что душе угодно, то можно повращать, поудлинять и ещё чего-нибудь поделать, получив в результате бесконечно мого решений. Поэтому я и просил автора четко сформулировать задачу и привести его три решения.

Мне представляется, что в самом первом письме Виктор вполне четко сформулировал задачу.
По крайней мере, я (возможно, в силу своей ограниченности) понял поставленную задачу однозначно.

Поясню, что имел в виду я, говоря нескольких возможных решениях:
Возьмем точки $ A(0;0), B(6;0), C(10;4), E(7;1) $. Для этого расположения точек существует три возможных положения точки D таких, что прямые AB и СD будут параллельны, а прямая, проходящая через C, параллельно AE, пересечет прямую AD в точке F, для которой $DF = BE$. Одно из этих положений ($D(4;4)$) приводит к параллелограмму, другое ($D(6-\sqrt{34};4)$) - к трапеции, третье (не вполне полноценное $D(6+\sqrt{34};4)$) - к самопересекающемуся четырехугольнику ABCD.

При других положениях точек A, B, C, E (причем E на отрезке BC) подходящих положений точки D может быть и больше. Но не больше четырех.

[gris]

Уважаемый VAL, обратите внимание, что в условии говорится не о параллельности сторон, а о сумме углов. В Вашем третьем случае они уже становятся накрест лежащими. И равны друг другу, являясь острыми. Если же рассматривать самопересекающиеся ломаные, то там стороны не обязательно будут параллельны.

[TOTAL]

Давайте все-таки уточним формулировку.
Длина стороны $AD$ и углы, прилегающие к ней (сумма их равна 180), фиксированы.
Длины отрезков $BE$ и $DF$ совпадают и равны заданному числу.
Где вершины $B$ и $C$? - Ответов бесконечно много.

Зафиксируем еще положение точки $B$ или точки $C$ или наклон пряиой $AE$. Сколько теперь решений?

[VAL]

gris писал(а):

обратите внимание, что в условии говорится не о параллельности сторон, а о сумме углов. В Вашем третьем случае они уже становятся накрест лежащими.

Согласен. Я ведь изначально говорил о четвертом решении, как о неполноценном. Но три хороших решения вполне возможны. Например, для точек $ A(0;0), B(7;0), C(11;4), E(8;1) $ существуют три положения точки D на прямой, проходящей через С параллельно AB, приводящие к нормальным четырехугольникам: параллелограмму и двум трапециям (у одной основание CD меньше AB, а у другой - больше. Координаты возможных положений вершины D не привожу лишь из-за их громоздкости (кроме случая параллелограмма, конечно).

Добавлено спустя 50 минут 57 секунд:

TOTAL писал(а):

Давайте все-таки уточним формулировку.

Это чревато окончанием плодотворной дисуссии

Цитата:

Длина стороны $AD$ и углы, прилегающие к ней (сумма их равна 180), фиксированы.

В приведенных мной примерах длина AD менялась. Но это не принципмально. Можно было зафиксировать точки A,D,C,F, а двигать точку B (тогда E тоже будет перемещаться). Тогда приведенные мной примеры сохранят свою силу после переименования точек.

Цитата:

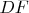
Длины отрезков $BE$ и $DF$ совпадают и равны заданному числу.
Где вершины $B$ и $C$? - Ответов бесконечно много.

Конечно! Но это явно не то, что интересовало Виктора. Интерес вызывает случай, когда параллелограмм, удовлетворяющий условию задачи задан однозначно. А вот сколько при этом подходящих четырехугольников - это и есть вопрос, который меня заинтересовал.

Цитата:

Зафиксируем еще положение точки $B$ или точки $C$ или наклон пряиой $AE$. Сколько теперь решений?

Если зафиксировать С, а смещать B (так чтобы AB оставалась параллельна CD) и не рассматривать самопересакающиеся четырехугольники, то не более трех. Но три вполне возможны, см. выше.

[gris]

посыпаю голову пеплом и каюсь. Ну не хватило 10 минут написать уравнение. Оно действительно 4-той степени. И в последнем примере VAL имеет 4 действительных корня. Из них три соответствуют выпуклому 4-х угольнику.
В знак раскаяния привожу уравнение для точки D(d;4):

$$(d^2+16)(d-11)^2=2(32-d)^2$$

.
Его график заставляет пролить слезу. Три точки:
D(-0.4;4) D(4;4) D(5.4;4) (приближенно).4-ый корень относится уже к самопересекающейся ломаной.

[vikzab]

Если представить прямые AB и AE в полярных координатах с началом полярных координат в точке С и параллельно АЕ (т.е. ось с 0 углом будет проходить по продолжению прямой СF), то можно записать их разницу (в частном случае это будет отрезок ВЕ):
a/(Cos[x - Pi/2 - b]) - c/(Cos[x - Pi/2]), 0<x<Pi, a>c>0, 0<b<Pi/2.
Если нарисовать данную кривую в программе Mathematica, то подставляя различные значения параметров a,с,b можно увидеть что корней может быть от 1 до 3, как ,например, в данном сочетании параметров:
Plot [2/(Cos[x - Pi/2 - 0.1]) - 1/(Cos[x - Pi/2]), {x, 0, Pi}, PlotRange -> Automatic,GridLines -> Automatic]

[vikzab]

TOTAL писал(а):

Давайте все-таки уточним формулировку.
Длина стороны $AD$ и углы, прилегающие к ней (сумма их равна 180), фиксированы.
Длины отрезков $BE$ и $DF$ совпадают и равны заданному числу.
Где вершины $B$ и $C$? - Ответов бесконечно много.

Зафиксируем еще положение точки $B$ или точки $C$ или наклон пряиой $AE$. Сколько теперь решений?

Важно не количество ответов в числовой форме, а при каких параметрах и какие в результате соблюдения заданных условий получатся геометрические фигуры. Вот, что хотелось бы увидеть в решении.

[gris]

Изначальная задача интересная, я бы даже сказал, красивая. Для меня результат был несколько неожиданным. Но так как мы выяснили, что при некотором уточнении условий, в некотором частном случае получается уравнение 4-й степени относительно свободного параметра, которое имеет 4 действительных корня, имеющих очень даже наглядный геометрический смысл, то чего ж Вам боле?
Дальнейшее развитие темы сведётся с исследованию кубических уравнений, поскольку один корень всегда есть. Если Вас действительно заинтересовада эта задача, то самое простое, как мне кажется, решать ее в прямоугольной системе координат, фиксируя не углы, а точки, и оставляя одну из вершин подвижной. Надо будет всего лишь отыскать координаты точки пересечения двух прямых и квадрат расстояния между двумя точками.
Получившееся уравнение будет иметь действительный корень, отвечающий параллелограмму. Разделив на соответствующий двучлен, мы получим уравнение третьей степени. Оно тоже заведомо имеет действительный корень, возможно, совпадающий с первым. Но там уже можно исследовать производную кубического многочлена и по ней определить число решений.
Но будет ли в этом исследовании какой-то смысл? Впрочем, может именно тут таится путь к элементарному доказательству Великой и Ужасной...

Добавлено спустя 9 минут 18 секунд:

Кстати, если начать расширять условия, например, считать углы при стороне АD не обязательно внутренними, то стороны АВ и CD уже могут быть не параллельными. Правда в этом случае придется считать точки Е и F лежащими не на сторонах, а на продолжениях сторон. Зато возникают невыпуклые четырехугольники и дополнительные решения. Так что без четко сформулированного условия, где будет указано... все это уже говорилось... не обойтись.