Определение понятия «отображение»:
Цитата:
Отображением множества

в множество
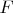
, или функций, определённой на

со значениями в
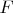
, называется правило, или закон

, который каждому элементу

ставит в соответствие определённый элемент

.
Определение понятия «инъективное отображение»:
Цитата:
Отображение

называется инъективным, если

или если

уравнение
 имеет не более одного решения
имеет не более одного решенияИз второго определения следует, что допускается существование

такого, что не найдется ни одного

, при котором бы выполнялось равенство

. Проще говоря такое равенство бы не имело решений.
Получается, что нельзя называть
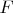
множеством значений функции

в случае инъективного отображения, так как это множество может содержать элементы, к которым нельзя поставить в соответствие

с помощью закона

?