СОКАКУ писал(а):
ddn писал(а):
Я так понимаю это ваша лучшая оценка, но если

и

,

. Тогда что


,

,

Хм...
СОКАКУ писал(а):
ddn писал(а):
Тогда

.
Совершенно не понятно почему a может ограничивать сверху

.( видно что именно так вы и поступали).Левое неравенство в условии ,совершенно очевидно, не верно для каждого i. Хотя конечно ошибки на этом не заканчиваются.
Этот вывод опирался на:

при

.
Теперь вижу, что в условии

неравенство стоит для фиксированного

, а не любого

(иначе условие противоречиво).
То есть

применимо лишь для

.
Тогда идем первоначальным путем


где

, так как

при


![$=(e\cdot\sqrt[k]{ek}\cdot a)^k\leqslant(e\cdot e\cdot a)^k<(4^{\frac{1}{\ln(2)}}\cdot a)^k<(4\cdot a)^{2^k-1}$ $=(e\cdot\sqrt[k]{ek}\cdot a)^k\leqslant(e\cdot e\cdot a)^k<(4^{\frac{1}{\ln(2)}}\cdot a)^k<(4\cdot a)^{2^k-1}$](https://dxdy-03.korotkov.co.uk/f/6/f/b/6fbcbc5475559183d56ef0995e2f4f3882.png)
учли еще, что

,

,
![$\sqrt[k]{ek}\leqslant\sqrt[1]{e}=e$ $\sqrt[k]{ek}\leqslant\sqrt[1]{e}=e$](https://dxdy-04.korotkov.co.uk/f/3/7/8/3786bed8f42825edb0dd3cdc8a302fa382.png)
и

Еще моя ошибка в том, что условие

,
в действительности лишь достаточно (но не необходимо) для существования

, требуемых условием.
Оно лишь гарантирует их наличие, но требуемые

могут существать (и существуют, как показал Ваш пример) и при

(в вашем примере

).
Неравенство

, таким образом, доказано для более узкой области значений
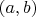
, чем требуется.
Если данное неравенство и верно при

,
то его доказательство существенно усложняется дискретностью значений

.
Думаю, без глубоких теорем теории чисел здесь ничего не доказать.