Spook писал(а):
AD... Что у Вас обозначает символ

(я лично встречал его как функцию Дирихле, либо как характеристическую функцию)?
Судя по всему это характеристическая:

Spook писал(а):
ddn писал(а):
Без бесконечного числа вариаций не обойтись.
Мне не знаком этот термин... у нее больше одного минимума?
Не просто больше одного, а бесконечное число. Под "бесконечным числом вариаций" я подразумевал бесконечную смену участков возрастания и убывания, и, значит, бесконечное число локальных максимумов и минимумов, которые сгущаются вблизи граничных точек интервала.
Пусть функция непрерывна на компакте из
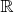
(связный компакт = замкнутый интервал) и имеет производную всюду на этом компакте - и функция, и производная со значениями в
![$\mathbb{\bar R}=[-\infty,+\infty]$ $\mathbb{\bar R}=[-\infty,+\infty]$](https://dxdy-02.korotkov.co.uk/f/5/3/4/5349b36204cfa3702d63d84e20d74c0282.png)
.
Spook писал(а):
по-моему, Вы хотите сказать, что либо функция неограничена, но монотонна и с неограниченной производной, либо ограничена, с конечной неограниченной производной, но у нее больше одного минимума. Это так?
Она (производная) может быть и ограниченной монотонной. Но если производная неограниченна на компактном интервале, то вблизи точки, где производная неограниченна, она (производная)
- либо бесконечна, и тогда она: разрывна либо непрерывна, монотонна в некоторой окрестности либо бесконечно варьируется (любые варианты);
- либо конечна, но тогда она разрывна (так как хотя бы один их ее пределов, правый или левый, не существует) и бесконечно варьируется.
Замечание: если в некоторой точке функция принимает бесконечное значение, то в некоторой ее окрестности она не должна иметь бесконечных значений того же знака (иначе производная в точке неопределена), а значение ее производной в такой точке - бесконечно, причем разных знаков с разных сторон. Поэтому, в некоторой окрестности такой точки, компакт должен иметь точки только по одну сторону от этой точки.
Здесь не рассмотрен случай сингулярных функций, производные которых правильно интегрируются (дают саму функцию) только Лебегом или Данжуа, или вообще не интегрируются. Но к монотонным производным это не относится.
Spook писал(а):
ddn,AD, правильно ли я понял, что у вас противоположные мнения по поводу существования искомой функции?
Почему же? Просто
AD предложил другой вид функции.