Дисперсия оценки параметра

[Mikhail Volkov]

Суть проблемы

Наблюдаем в дискретном времени случайный процесс:
$x_k = Ax_{k-1} + w_k, \quad w_k \sim \boldsymbol{N}(0, \boldsymbol{Q}(\mu))$
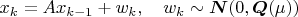
Наблюдаем вот так:
$z_k = H x_k + v_k, \quad v_k \sim \boldsymbol{N}(0, \boldsymbol{R})$
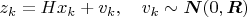
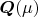
У $w_k$ корреляционная матрица $\boldsymbol{Q}(\mu)$ зависит от одного скалярного параметра. Он неизвестен.

И я с помощью банка фильтров Калмана, настроеных на дискретный набор значений параметра $\mu$ пытаюсь оценить, чему равен этот параметр, для чего для каждого фильтра Калмана вычисляется логарифм функции правдоподобия. Оценка параметра берется по максимуму логарифма функции правдоподобия среди всех фильтров.

Можно ли посчитать ошибку оценки параметра как-то еще помимо моделирования Монте-Карло, которое достаточно медленно сходится? По Монте-Карло я считаю.

[dsge]

Как обычно для метода максимума правдоподобия - считается Гессиан в максимуме функции лог-правдоподобия, обращается, умножается на -1, на диагонале будут стоять дисперсии оценок параметров.

[Mikhail Volkov]

Удалось посчитать границу Рао-Крамера, посчитав матожидание логарифма функции правдоподобия и затем (численно) продифференцировав это матожидание по параметру:
$I_{ij}(\mu)=E\left\lbrace \frac{\partial L(\mu \left\lvert z_{1:N})}{\partial \mu_i} \frac{\partial L(\mu \left\lvert z_{1:N})}{\partial \mu_j} \right\rbrace = - E\left\lbrace \frac{\partial^2 L(\mu \left\lvert z_{1:N})}{\partial \mu_i \partial \mu_j} \right\rbrace=$
$= - \frac{\partial^2}{\partial \mu_i \partial \mu_j} E\left\lbrace L(\mu \left\lvert z_{1:N}) \right\rbrace$
$I_{ij}(\mu)$ - элемент информационной матрицы Фишера.

!!!!!! Матожидание логарифма функции правдоподобия $E\left\lbrace L(\mu \left\lvert z_{1:N}) \right\rbrace$ зависит не только от $\mu$, но и от истинного значения параметра $\mu_0$

[Mikhail Volkov]

Правда, есть один момент, который меня настораживает. Мне тут попалась одна работа, где информационную матрицу Фишера считают вот так:
$I_{ij}(\mu)= - E\left\lbrace \frac{\partial^2 L(\mu \mid z_{1:N})}{\partial \mu_i \partial \mu_j} \right\rbrace = \sum\limits_{i=1}^{N} \operatorname{tr} \left\lbrace \frac{1}{2} S_k^{-1} \frac{\partial S_k}{\partial \mu_i} S_k^{-1} \frac{\partial S_k}{\partial \mu_j} + S_k^{-1} E\left\lbrace \frac{\partial e_k}{\partial \mu_i} \frac{\partial e_k^T}{\partial \mu_j} \right\rbrace \right\rbrace$
где $S_k = H P_{ k \mid k-1 } H^T + R, \quad e_k = z_k - H x_{ k \mid k-1 }$

Исходный логарифм функции правдоподобия выглядит вот так:
$L(\mu \mid z_{1:N}) = - \frac{N p}{2}\ln(2 \pi) - \frac{1}{2} \sum\limits_{i=1}^{N} e_k^T S_k^{-1} e_k $

Т.е. зачем-то усложняют себе жизнь, вычисляя матожидание гессиана логарифма функции правдоподобия, а не гессиан матожидания логарифма функции правдоподобия. И далее все это приводит к сложным громоздким рекурсивным выражениям.

Зачем так усложнять себе жизнь? Мы же вроде как вполне законно поменяли местами операции матожидания и взятия производной. Или нет?