Во что вырождаются биномиальные коэффициенты?

[Predictor]

Четыреномиальные коэффициенты $K_n^{i,j,k,l}$ при i, или j, или k, или l равном нулю вырождаются в триномиальные. Триномиальные: $ T_n^{i,j,k} $ вырождаются в биномиальные, а биномиальные вырождаются в 1. Т.е. $C_n^0$ не является по этой аналогии биномиальным коэффициентом, как и $C_n^n$. Эти биномиальные коэффициенты вырождаются в монономиальный коэффициент, равный 1. Вырождение происходит потому, что мы берем пустое множество, а оно особенное в сравнении с непустыми. И последний этап вырождения наблюдается у биномиальных коэффициентов в 1 при любом $n\in\mathbb N$. Т.е. единицы из треугольника Паскаля по идее следует исключить.
У биномиальных коэффициентов вида $C_{2n}^n$ нет симметричного партнера как у всех остальных. Чтобы соблюсти симметрию и однородность в свойствах коэффициентов его следует удвоить? или разделить на 2 равные части? Или исключить? Наверное надо пробовать все варианты и искать закономерности?

[Евгений Машеров]

Зачем?

(Оффтоп)

Андрей Вознесенский, вас сюда не звали!

-- 18 фев 2026, 06:18 --

Коэффициент закономерно равен единице. Потому, что $0! =1$

[Predictor]

Евгений Машеров в сообщении #1718499 писал(а):

Зачем?

Чтобы посмотреть, что из этого может выйти.

Евгений Машеров в сообщении #1718499 писал(а):

Коэффициент закономерно равен единице. Потому, что $0! =1$

Но можно сказать и 0! приняли равным единице для того, чтобы выполнялся ряд закономерностей, в том числе и с биномиальными коэффициентами. Но это же не опровергает того факта, что $C_n^0$ вырожденный в монономиальный биномиальный коэффициент. И не исключает возможности для поиска других смыслов и закономерностей.

(Оффтоп)

Евгений Машеров в сообщении #1718499 писал(а):

Андрей Вознесенский, вас сюда не звали!

(Оффтоп)

Если бы мы не появлялись в тех местах в которые нас не звали, то, пожалуй, нас бы и не было. Но раз уж мы все-таки существуем в этом мире, то значит кто-то нас сюда позвал)

[TOTAL]

(Оффтоп)

Predictor в сообщении #1718490 писал(а):

Четыреномиальные коэффициенты $K_n^{i,j,k,l}$ при i, или j, или k, или l равном нулю вырождаются в триномиальные.

Сумма четырёх слагаемых $i+j+k+l}$ при i, или j, или k, или l равном нулю вырождаются в сумму трёх слагаемых. Или не вырождается, а просто одно слагаемое равно нулю?

[Predictor]

TOTAL в сообщении #1718515 писал(а):

(Оффтоп)

Predictor в сообщении #1718490 писал(а):

Четыреномиальные коэффициенты $K_n^{i,j,k,l}$ при i, или j, или k, или l равном нулю вырождаются в триномиальные.

Сумма четырёх слагаемых $i+j+k+l}$ при i, или j, или k, или l равном нулю вырождаются в сумму трёх слагаемых. Или не вырождается, а просто одно слагаемое равно нулю?

Нулевое слагаемое не влияет на сумму, поэтому его можно отбросить. При этом наверное не будет ошибкой сказать, что сумма четырех слагаемых выродилась в сумму трех.

-- 18.02.2026, 11:10 --

Еще одно замечание про мультиномиальные коэффициенты: существует лишь единственный $\infty$-номиальный коэффициент и он имеет вид: $C_{\infty}^{1,1,1,1,1,1,1,1,1,.........}$ и он равен $\infty!$, Сумма биномиальных коэффициентов из бесконечности равна ${2^{\infty}$. Эти понятия неопределенные, но в некоторой степени интуитивно понятные. $1, 2^{\infty},\infty!$. Теперь возникает вопрос чему будет равна аналогичная сумма триномиальных, четыреномиальных и т.д. коэффициентов и как происходит переход от $2^{\infty}$ к $\infty!$.

[dgwuqtj]

Predictor в сообщении #1718516 писал(а):

существует лишь единственный $\infty$-номиальный коэффициент и он имеет вид: $C_{\infty}^{1,1,1,1,1,1,1,1,1,.........}$ и он равен $\infty!$

А что не так с $C_\infty^{2, 1, 1, \ldots} = \frac {\infty!} 2$?

[Predictor]

dgwuqtj в сообщении #1718522 писал(а):

Predictor в сообщении #1718516 писал(а):

существует лишь единственный $\infty$-номиальный коэффициент и он имеет вид: $C_{\infty}^{1,1,1,1,1,1,1,1,1,.........}$ и он равен $\infty!$

А что не так с $C_\infty^{2, 1, 1, \ldots} = \frac {\infty!} 2$?

Здесь есть трудности с записью и сомнения. Необходимо, как мне кажется, количество верхних индексов уменьшить на 1, т.е. их должно стать $\infty-1$, непонятно как это записать. Понятно, что это лишь значение одного коэффициента, поэтому, чтобы найти сумму, необходимо умножить это значение на $\infty-1$. получится $\frac {(\infty-1)\infty!} {2}$

[Predictor]

Такая еще мысля пришла: $n^{\infty}$ - это сумма n-номиальных коэффициентов из бесконечности, которые в классическом случае включают и коэффициенты низших номиальностей, т.е. по сути вырожденные коэффициенты. Чтобы получить чистые n-номиальные коэффициенты, необходимо исключить вырожденные. Рассмотрим пирамиду Паскаля для триномиальных коэффициентов: . На ее ребрах расположены монономиальные коэффициенты, на гранях- биномиальные, а собственно чистые триномиальные коэффициенты располагаются в объеме пирамиды. При этом сумма коэффициентов n-ного слоя пирамиды равна $3^n$. Отсюда следует вычесть биномиальные коэффициенты n-ного слоя, включающие монономиальные. Т.к. граней у пирамиды 3, то вычесть "грязные" биномиальные коэффициенты придется 3 раза, но т.к. каждое ребро принадлежит 2-м граням, то получится, что мы вычтем монономиальные коэффициенты дважды и их необходимо будет вернуть назад. Итого, сумма чистых триномиальных коэффициентов $\infty$- слоя равна $3^{\infty}-3\cdot 2^{\infty}+3$.

Ну и раз уж пошла такая пьянка, то есть предположение, что мультиномиальные коэффициенты укладываются в n-симплексе и чтобы находить "чистые", необходимо действовать методом включений-исключений. Хотя это и не приближает к пониманию как происходит последовательный переход от $n^{\infty}$ к $\infty !$.

[Predictor]

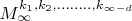
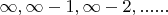
Еще, чтобы более детально исследовать вопрос, предлагаю ввести для $\infty$- номиальных коэффициентов такую нотацию: $M_{\infty}^{k_1,k_2,........,k_{\infty-d}$, тогда можно увидеть, что т.к. мы оперируем натуральными числами и их счетное множество, то мы имеем ограничение на количество math]$\infty, \infty- 1, \infty- 2,...... $[/math]- номиальных коэффициентов. 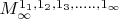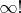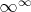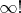Так мы убедились, что $\infty$- номиальный коэффициент всего 1: $M_{\infty}^{1_1,1_2,1_3,.....,1_{\infty}$ и он равен $\infty!$, в то время как сумма $n$- номиальных коэффициентов от бесконечности равна $n^{\infty}$, если бы закономерность сохранялась, то сумма $\infty$- номиальных коэффициентов от счетного множества была бы равна $\infty^{\infty}$, а не $\infty !$, что, согласитесь, не одно и то же. Причем чем больше конечная номиальность, тем больше коэффициентов от бесконечности у нее, но когда мы переходим к бесконечным и околобесконечным номиальностям, то наблюдается уменьшение количества коэффициентов вплоть до одного на бесконечной номиальности. Т.е. закономерности, наблюдаемые в области конечных номиальностей не выполняются для бесконечных номиальностей. Однако ИИ выдает информацию о том, что мощность факториала счетного множества равна континууму: $\aleph !=2^{\aleph}$. 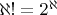Я этого понять и принять не могу!

Грубо и образно говоря вот есть у нас $\infty$-симплекс, заполненный мультиномиальными коэффициентами. когда мы рассматриваем его n-грани, то видим, что с каждым этажом, что видно на пирамиде выше, сумма мультиномиальных коэффициентов увеличивается в n- раз, а их количество растет. Но если мы берем бесконечные номиальности, т.е. весь $\infty$-симплекс, то на его бесконечном этаже всего 1 мультиномиальный коэффициент и их количество возрастает при переходе к предбесконечным номиальностям, т.е. при уменьшении номиальности - это обратный конечным номиальностям процесс. Значит есть где-то граничные точки или граничные номиальности, где процесс меняет направление. Или надо как-то обосновать эту смену направления процесса.