Неприводимость полинома в Q[x]

[Dedekind]

Доказать, что полином $x^4 - 10x^2 + 1$ неприводим в $\mathbb{Q}[x]$.

Можно проверить отсутствие рациональных корней (то есть, отсутствие множителей первой степени), а затем доказать, что и множителей второй степени быть не может.

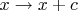
Но в задании предполагается, что его нужно сделать заменой вида $x \to x+c$ и затем применением критерия Эйзенштейна. Но я что-то сходу нужную замену подобрать не могу. Другие задания в этом блоке вроде были сразу очевидны, поэтому вопрос: действительно ли тут можно по Эйзенштейну?

[nnosipov]

Dedekind в сообщении #1718088 писал(а):

действительно ли тут можно по Эйзенштейну?

Нельзя: раскройте скобки в $(x+c)^4-10(x+c)^2+1$ и подумайте, каким могло бы быть простое число $p$ из критерия Эйзенштейна.

Этот многочлен является типичным примером многочлена, неприводимого над $\mathbb{Q}$, но приводимого над любым $\mathbb{Z}_p$: все дело в том, что

$$x^4-10x^2+1=\prod (x \pm \sqrt{2} \pm \sqrt{3}).$$

[Dedekind]

nnosipov
Спасибо! У меня в итоге получилось так: замена $x \to 2x+1$ и затем критерий Эйзенштейна (дуальный).