Доказал ли Эндрю Уайлз "Великую теорему Ферма"?

[AleksandrBegemot]

В рунете есть мнение о том, что уравнение в формулировке теоремы: $a^n+b^n=c^n$ есть общий вид функционального алгоритма: $c=f(x)=\sqrt[n]{a^n+b^n}$.

Это подразумевает, при доказательстве теоремы, в самом начале доказательства, артикуляцию обоих знакопеременных варианта:
$c=f(x)=\sqrt[n]{a^n+b^n}$;
$c=f(x)=\sqrt[n]{a^n-b^n}$.

Поэтому, целочисленность двух задаваемых независимых аргументов: $a$ и $b$, выбираемых произвольно, не подвергается сомнению. В доказательстве целочисленности
нуждается результат функционального вычисления. Но функций, в этом случае, образуются две , а не одна:

1. $c=f(x)=\sqrt[n]{a^n+b^n}$;
2. $k=f(x)=\sqrt[n]{a^n-b^n}$.

То есть, для математической полнотты доказательства необходимо рассмотреть две тройки чисел:

1. $a^n+b^n=c^n$;
2. $k^n+b^n=a^n$.

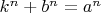
Это предgоложение совдает с формулой Эвклида для нахождения всех возможных троек для $n=2$:

$(2\cdot x\cdot y)^2+(x^2-y^2)^2=(x^2+y^2)^2$,
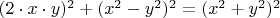
которая будет выглядеть в других обозначениях как

$(2\cdot a\cdot b)^2+(k^2)^2=(c^2)^2$.

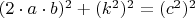
В альтернативном варианте, на некотором сайте, формула общего вида выглядит так:

$(\sqrt[n]{4}\cdot x\cdot y)^n+(k^2)^n=(c^2)^n$.

Нецелочисленность результата в случае применения $n>2$ обеспечивается множителем $\sqrt[n]{4}$, результат которого будет гарантированно нецелочисленным в этом случае: $1<\sqrt[n]{4}<2$.

Возможно, я чего-то недопонял или сделал ошибки или описки в тексте, но мне, главное, было передать основную мысль. Хочу увидеть мнение завсегдатаев форума.

[EUgeneUS]

AleksandrBegemot в сообщении #1717261 писал(а):

Эвклида

В русскоязычной традиции принято "Евклид", а не "Эвклид".

AleksandrBegemot в сообщении #1717261 писал(а):

В рунете есть мнение о том, что уравнение в формулировке теоремы: $a^n+b^n=c^n$ есть общий вид функционального алгоритма:

Цитата:

Функциональный алгоритм

Частный алгоритм, реализующий одну или несколько функционально законченных задач преобразования информации

Источник: ОСТ 1 00189-82: Системы бортовые цифровые вычислительные. Состав документов по алгоритмам и программам

И причем тут Эндрю Уайлз и Великая теорема Ферма?
Не читайте мнения на заборах в рунете.

[AleksandrBegemot]

EUgeneUS в сообщении #1717262 писал(а):

AleksandrBegemot в сообщении #1717261 писал(а):

Эвклида

В русскоязычной традиции принято "Евклид", а не "Эвклид".
И причем тут Эндрю Уайлз и Великая теорема Ферма?

Благодарю за Ваше эксклюзивное мнение о философии. По теме поста ничего сказать не сможете?

[dgwuqtj]

AleksandrBegemot в сообщении #1717261 писал(а):

Это подразумевает, при доказательстве теоремы, в самом начале доказательства, артикуляцию обоих знакопеременных варианта:

Откуда второй вариант?

[AleksandrBegemot]

AleksandrBegemot в сообщении #1717261 писал(а):

В рунете есть мнение о том, что уравнение в формулировке теоремы: $a^n+b^n=c^n$ есть общий вид функционального алгоритма: $c=f(x)=\sqrt[n]{a^n+b^n}$.

Это подразумевает, при доказательстве теоремы, в самом начале доказательства, артикуляцию обоих знакопеременных варианта:
$c=f(x)=\sqrt[n]{a^n+b^n}$;
$c=f(x)=\sqrt[n]{a^n-b^n}$.

Сам увидел описку:

$c=f(a, b)=\sqrt[n]{a^n+b^n}$;
$k=g(a,b)=\sqrt[n]{a^n-b^n}$.

[Mikhail_K]

AleksandrBegemot в сообщении #1717263 писал(а):

По теме поста ничего сказать не сможете?

Отчего же, можно. В посте написана какая-то невнятная ерунда.

[EUgeneUS]

AleksandrBegemot в сообщении #1717263 писал(а):

о теме поста ничего сказать не сможете?

Так было же сказано.
Могу повторить более развернуто: стартовый пост - шизофазия.

[AleksandrBegemot]

EUgeneUS в сообщении #1717271 писал(а):

AleksandrBegemot в сообщении #1717263 писал(а):

о теме поста ничего сказать не сможете?

Так было же сказано.
Могу повторить более развернуто: стартовый пост - шизофазия.

Разверните

[Gagarin1968]

AleksandrBegemot в сообщении #1717272 писал(а):

Разверните

Разворачиваю.
Автор темы, как я уже тут упоминал, известный пациент, тролль и антисемит Сергей Мишин.
Вот доказательства: здесь и тут.
Да и стиль дискуссии не поменялся.

[Mikhail_K]

AleksandrBegemot в сообщении #1717272 писал(а):

Разверните

Там нечего разворачивать. Аргументация неразумна и невнятна, комментировать в ней нечего.

[Ende]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Пургаторий (М)»
Причина переноса: бред.

AleksandrBegemot - постоянный бан за хроническую бредогенерацию.