Задача на двойной интеграл от модуля

[IIILUXA]

Привожу текст задачи:
Пусть $g(x)$ - непрерывная функция, заданная на отрезке $[0,1]$. Верно ли, что:

$$\int_0^1 \int_0^1 |g(x)+g(y)| dxdy \geq \int_0^1 |g(x)| dx$$

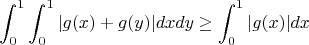
Контрпример подобрать так и не получилось, так что я пробовал доказать неравенство. Моя идея была в следующем: непонятно, как сравнивать одномерный интеграл с двумерным, поэтому стоит попробовать перейти к более похожим объектам:

$$\int_0^1 |g(x)| dx = 1 \cdot \int_0^1 |g(x)| dx = \int_0^1 dy \cdot \int_0^1 |g(x)| dx = \int_0^1 \int_0^1 |g(x)| dxdy = $$ $$ = \int_0^1 \int_0^1 |\frac{g(x)+g(y)}{2} + \frac{g(x)-g(y)}{2}| dxdy $$

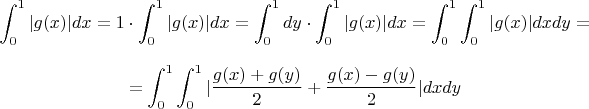
Теперь воспользуемся неравенством треугольника:

$$ |\frac{g(x)+g(y)}{2} + \frac{g(x)-g(y)}{2}| \leq |\frac{g(x)+g(y)}{2}| + |\frac{g(x)-g(y)}{2}| $$

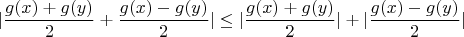
Кроме того,

$$ |g(x)+g(y)| = |\frac{g(x)+g(y)}{2}| + |\frac{g(x)+g(y)}{2}| $$

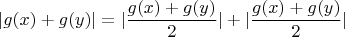
Отсюда уже видно, что если верно неравенство

$$\int_0^1 \int_0^1 |g(x)+g(y)| dxdy \geq \int_0^1 \int_0^1 |g(x)-g(y)| dxdy, $$

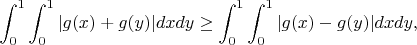
то верно и исходное неравенство. Здесь уже сравниваемые объекты более похожи друг на друга и как будто более интуитивно понятно, что неравенство верно, однако мне так и не удалось его доказать. Буду благодарен, если кто-то подскажет идею.

[Mr. X]

Верно, не просто, Putnam 2003.