Стандартная равновесная термодинамика.
Рассмотрим термодинамический процесс, описываемый на плоскости

простой прямой
![$L[AB]$ $L[AB]$](https://dxdy-01.korotkov.co.uk/f/4/a/c/4ac2e38454559ec3b5b3fc0b2f9d93dc82.png)
, которую можно описывается одновременно двумя способами:
![$ L[AB] \, := \, \{ (T,V): \quad T \in [T_1,T_2] , \quad V \, = \, V(T) \} , $ $ L[AB] \, := \, \{ (T,V): \quad T \in [T_1,T_2] , \quad V \, = \, V(T) \} , $](https://dxdy-04.korotkov.co.uk/f/3/1/c/31c3e81c57e916829e216468c05f888d82.png)
![$ L[AB]\, := \, \{ (T,V): \quad V \, \in \, [V_1,V_2] , \quad T \, = \, T(V) \} , $ $ L[AB]\, := \, \{ (T,V): \quad V \, \in \, [V_1,V_2] , \quad T \, = \, T(V) \} , $](https://dxdy-03.korotkov.co.uk/f/6/8/e/68e1bc0830724d447c76e0c19d8d6bb682.png)
где

и

— непрерывно дифференцируемые функции, и
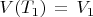
, и
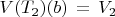
, так что
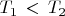
и
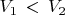
.
Изменение теплоты
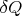
обычно записывают в виде
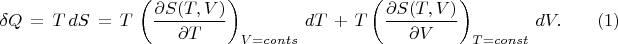
Количество тепла

можно записать в виде
![$$ Q \, = \, \int_{L[AB]} \Bigl(
T \, \left(\frac{\partial S(T,V)}{\partial T} \right)_{V} \, dT \, + \,
T \, \left(\frac{\partial S(T,V)}{\partial V} \right)_{T} \, dV \Bigr) \, = \,
$$ $$ Q \, = \, \int_{L[AB]} \Bigl(
T \, \left(\frac{\partial S(T,V)}{\partial T} \right)_{V} \, dT \, + \,
T \, \left(\frac{\partial S(T,V)}{\partial V} \right)_{T} \, dV \Bigr) \, = \,
$$](https://dxdy-03.korotkov.co.uk/f/6/8/8/688b217c373364efcb8b5668ab6163e382.png)
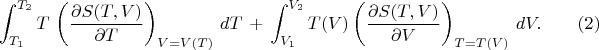
Воппос 1: Правильно ли записано выражние (2) ?
По моему Да.
Вопрос 2: Можно ли записать уравнение (1) для этого термодинамического процесса в виде
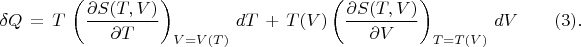
По моему Да.
А может я не прав, и что-то nen не так?