Определение пучка на сайте

[OlgaD]

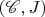
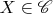
Я пытаюсь разобраться, что такое пучок на сайте $(\mathscr{C},J)$ относительно топологии Гротендика $J.$ Мне встретилось лаконичное определение в Википедии (https://en.wikipedia.org/wiki/Grotendie ... nd_sheaves). Определение выглядит так: назовем пучком на сайте предпучок $F$ такой, что для всех объектов $X\in\mathscr{C}$ и всех покрывающих решет $S$ на $X$ естественное отображение

$$\mathrm{Hom}(\mathrm{Hom}(-,X),F)\to\mathrm{Hom}(S,F),$$

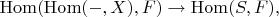
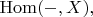
индуцированное включением $S$ в $\mathrm{Hom}(-,X),$ является биекцией.

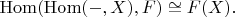
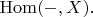
Я знаю, что по лемме Йонеды имеет место изоморфизм $\mathrm{Hom}(\mathrm{Hom}(-,X),F)\cong F(X).$ Так же знаю, что решето $S$ можно определить как подфунктор $\mathrm{Hom}(-,X).$ Т.е., выходит, в этой формуле сопоставляются естественные преобразования. Но до конца это сопоставление не понятно.

[dgwuqtj]

Вы понимаете, что такое пучок на топологическом пространстве?

[OlgaD]

Да, с этим понятием я знакома. Пучок на топологическом пространстве $X$ - это предпучок, для которого выполняются две аксиомы, существования и склейки.

[dgwuqtj]

Вот и тут что-то похожее, для любых элементов $y_s \in F(Y)$ при $(s \colon Y \to X) \in S$ существует единственный $x \in F(X)$, который в них переходит. В Википедии чуть ниже написано про предтопологии, это более конкретный способ описания решёт, и на практике обычно пользуются им. Скажем, для fppf или этальной топологии.

[OlgaD]

Извините, я не совсем поняла ваш ответ. Что вы подразумеваете под $x\in X?$

[dgwuqtj]

$x \in F(X)$, спасибо за замечание.

[OlgaD]

Если у нас есть изоморфизм $\mathrm{Hom}(\mathrm{Hom}(-,X),F)\cong F(X),$ то что такое $F(Y)?$ Ваш ответ очень лаконичен и мне совсем не понятен.

[dgwuqtj]

Решето $S$ — это какое-то множество морфизмов с концами в $X$. Для каждого морфизма $s \colon Y \to X$, принадлежащего $S$, выберем элемент $y_s \in F(Y)$. Тут $Y$ пробегает все объекты категории, а $s$ — все морфизмы из решета. Потребуем, чтобы $f^*(y_s) = z_{s \circ f}$ для каждого $s \colon Y \to X$ из решета и каждого морфизма $f \colon Z \to Y$. Тогда условие на пучок — это что существует единственный $x \in F(X)$ такой, что $y_s = s^*(x)$ при $s$ из решета. Через $f^*$ и $s^*$ я обозначил отображения $F(f)$ и $F(s)$, просто со звёздочкой не надо помнить про контравариантность и легче читать.