Это вам не Гурса!

[Red_Herring]

1. Найдите непрерывное в $(0,0)$ решение
\begin{align} &u_{tt}-u_{xx}=0 && k t> |x|,\\ &u|_{x= \pm kt} = \pm t^\alpha &&-\infty<x<\infty \end{align}
где $0< k< 1$ and $\alpha >0$.
2. Объясните, что случится без условия "непрерывное в $(0,0)$''.
3. Объясните, что случится при $\alpha\le 0$.
4. Объясните, что случится при $k\to 1^-$.

[Padawan]

1. $u(x,t)=C_1(t-x)^\alpha+C_2 (t+x)^\alpha$, где

$$C_1=-\frac{1}{1-\left(\frac{1-k}{1+k}\right)^\alpha}\cdot\frac{1}{(1+k)^\alpha},$$

$$ C_2=\left(\frac{1}{1-\left(\frac{1-k}{1+k}\right)^\alpha}-1\right)\cdot\frac1{(1-k)^\alpha}. $$

Вроде не ошибся. Граничным условиям удовлетворяет.

[Padawan]

2. Без условия непрерывности решений будет бесконечно много: $u=f(t-x)+g(t+x)$, где $f\colon (0,+\infty)\to\mathbb R$ -- любая функция, удовлетворяющая функциональному уравнению

$$ f\left(\left(\frac{1-k}{1+k}\right)^2 z\right)=f(z)+\left(1+\left(\frac{1-k}{1+k}\right)^\alpha\right)\left(\frac{z}{1+k}\right)^\alpha $$

для всех $z\in (0,+\infty)$. А функция $g$ выражается через функцию $f$ при помощи граничного условия.

[Red_Herring]

2. На самом деле все можно сформулировать еще проще: чтобы проверить единственность, надо проверить есть ли нетривиальные решения при нулевых граничных условиях, и тогда уравнение будет $f(rz)=f(z)$ т.е. $f(z)=\phi(\log (z)/\log(r))$ где $\phi$ периодическая функция с периодом 1.

[Padawan]

Red_Herring
А $r=\left(\frac{1-k}{1+k}\right) ^2$?

[Red_Herring]

Конечно

[vicvolf]

Вот что выдал DeepSeek

(Оффтоп)

1. $ u(x,t) = \frac{(t-x)^{\alpha} - (t+x)^{\alpha}}{(1-k)^{\alpha} - (1+k)^{\alpha}} \), \( kt > |x| \), \( \alpha >0 $.

2. Без условия непрерывности в (0,0) решение неединственно (можно добавить функцию, зануляющуюся на границах, но разрывную в нуле).

3. При $ \alpha \le 0 $ непрерывного в (0,0) решения не существует (при $ \alpha=0$ — противоречие в условиях, при $ \alpha<0 $ — бесконечность в нуле).

4. При $ k \to 1^- $ решение стремится к функции, но при $ k=1 $ задача задана на характеристиках и становится переопределённой или некорректной (решение существует не для всех $\alpha $ или неединственно).

[Red_Herring]

vicvolf
Это олимпиадная задача, а не проверка умения бездумного повторения неполных или неверных ответов ИИ. Рассуждения отсутствуют.

[Red_Herring]

Поскольку продолжения не последовало, то

1. Автомодельное решение правильно найдено Padawan при $\alpha\ne 0$

$$u(x,t)=\frac{(t+x)^\alpha - (t-x)^{-\alpha}}{(1+k)^\alpha - (1-k)^{-\alpha}}.$$

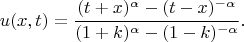
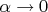
При $\alpha\to 0$ в пределе получаем опять-таки автомодельное решение при $\alpha= 0$:

$$u(x,t)=\frac{\log (t+x)/(t-x) }{\log (1+k)/(1-k)}}.$$

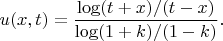
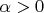
При $\alpha> 0$ это решение непрерывное в $(0,0)$, а при $\alpha= 0$ оно ограничено.

2. С единственностью разобрались.

3. Предел при $k\to 1^-$:
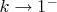
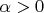
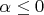
Он будет решением задачи Гурса при $\alpha> 0$ (которую DipShit назвал неправильно назвал некорректной), а вот при $\alpha\le 0$ предел будет $0$ внутри сектора, а вовсе не решением задачи Гурса, которая в этом случае решения иметь не будет.

[vicvolf]

Red_Herring в сообщении #1716825 писал(а):

Поскольку продолжения не последовало

На форуме не положено продолжать оффтоп, хотя DeepSeek выдал обоснование. Если интересно, то могу привести его в теме по ИИ?

[Red_Herring]

vicvolf в сообщении #1716865 писал(а):

На форуме не положено продолжать оффтоп, хотя DeepSeek выдал обоснование. Если интересно, то могу привести его в теме по ИИ?

Под проделжением я понимаю пост Padawan.

(Оффтоп)

А глупости DS бы и публиковали бы там с самого начал. Почему вам хочется гадить в темах, в которых вы абсолютно не разбираетесь?

[ozheredov]

(Оффтоп)

Red_Herring в сообщении #1716867 писал(а):

А глупости DS бы и публиковали бы там с самого начал. Почему вам хочется гадить в темах, в которых вы абсолютно не разбираетесь?

C ДикПиком ДипСиком все стали разбираться во всём. На форуме уже куча математиков, писателей, художников, погромиздов, знатоков-хоть-сейчас-за-стол-в-Охотничий-Домик и даже тим-лидеров. По факту же не понимают, что вот это

vicvolf в сообщении #1716865 писал(а):

Если интересно, то могу привести его в теме по ИИ?

утверждение, а не вопрос. Это и есть первобытное общество

[Red_Herring]

В продолжение:

Рассмотрим
\begin{align*} &u_{tt}- u_{xx}=0, && |x|< t+\varepsilon,\ t>0;\\ &u|_t=0, \quad u_t|_{t=0}=0 && |x|<\varepsilon;\\ &u|_{x=-t-\varepsilon}=-1, && u|_{x=t+\varepsilon}=1. \end{align*}
Имеется разрывное решение. К чему стремится это решение при $\varepsilon\to 0$?

(Оффтоп)

DeepSickу сдлова не давали.

[Red_Herring]

К первоначальной задаче\begin{tikzpicture} \clip (-6.5, -.5) rectangle (6.5, 18); \draw[ultra thin,->] (-6,0)--(6,0) node {$x$}; \draw[ultra thin,->] (0,0)--(0,18) node {$t$}; \draw[ultra thick] (-6,18)--(0,0)--(6,18); \draw[orange, ultra thick] (1,3)--(-2,6); \draw[blue, ultra thick] (-2,6)--(4,12); \draw[orange, ultra thick] (4,12)--(-8,24); \draw[blue, ultra thick] (-.5,1.5)--(1,3); \draw[orange, ultra thick] (.25,.75)--(-.5,1.5); \end{tikzpicture}
ко второй задаче
\begin{tikzpicture} \fill[green!30](-6.5,6)--(-.5,0)--(0, 0.5)--(-5.5,6); \fill[cyan!20](6.5,6)--(.5,0)--(0, 0.5)--(5.5,6); \draw[ultra thin,->] (-6,0)--(6,0)node {$x$}; \draw[ultra thin,->] (0,0)--(0,6) node {$t$}; \draw[ultra thick] (-6.5, 6)--(-.5,0)--(.5,0)--(6.5,6); \draw[ultra thin] (-5.5, 6)--(.5,0)--(-.5,0)--(5.5,6); \end{tikzpicture}