Добрый день.
В англоязычном учебнике по линейной алгебре предлагается доказать, что базисы линейного подпространства

из

содержат одинаковое число векторов.
Я зашел в тупик. Прошу подсказать дальнейшие шаги.
Пусть для подпространства

есть два базиса

и

. Нам нужно показать, что
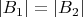
. Я начал показывать это по индукции по размеру

. Для случая, когда

содержит один вектор, а

содержит большее число векторов, я показал, что это невозможно. Но для случая
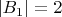
я не могу прийти к противоречию. Мне нужно как-то выразить один вектор
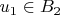
через другие векторы
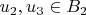
- это у меня не получается.