По мотивам одного числового равенства.

[Ruslan_Sharipov]

В мессенджере Teleram https://t.me/Pomatematike/3476 увидел равенство

$$1^3+2^3+3^3+\ldots+n^3=(1+2+3+\ldots+n)^2$$

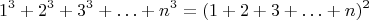
и возникла идея следующих задач.

Задача 1. Какие существуют полиномы $P(x)$ и $Q(x)$, чтобы выполнялось равенство

$$P(1)+P(2)+P(3)+\ldots+P(n)=(Q(n))^2\ \forall n\in\mathbb N?$$

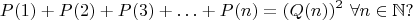Задача 2. Какие существуют полиномы $P(x)$ и $q(x)$, чтобы выполнялось равенство

$$P(1)+P(2)+P(3)+\ldots+P(n)=(q(1)+q(2)+q(3)+\ldots+q(n))^2\ \forall n\in\mathbb N?$$

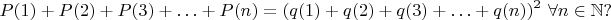Задача 3. Какие существуют полиномы $P(x)$ и $Q(x)$, чтобы при некотором фиксированном $s$ выполнялось равенство

$$P(1)+P(2)+P(3)+\ldots+P(n)=(Q(n))^s\ \forall n\in\mathbb N?$$

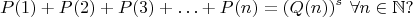Задача 4. Какие существуют полиномы $P(x)$ и $q(x)$, чтобы при некотором фиксированном $s$ выполнялось равенство

$$P(1)+P(2)+P(3)+\ldots+P(n)=(q(1)+q(2)+q(3)+\ldots+q(n))^s\ \forall n\in\mathbb N?$$

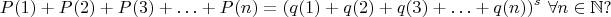
В задачах 3 и 4 случаи, когда $s$ не целое, тоже представляют интерес.

Я не знаю решения этих задач и не знаю какого они уровня, олимпиадного или выше. Я не знаю также встречались ли они где-либо ранее. Поэтому любая информация об этих задачах представляет интерес.

[ИСН]

На 1 ответ простой: $Q$ любой, а $P(n)=Q^2(n)-Q^2(n-1)$.
На все остальные примерно так же.

[Null]

ИСН в сообщении #1716383 писал(а):

На 1 ответ простой: $Q$ любой, а $P(n)=Q^2(n)-Q^2(n-1)$.

$Q(0)=0$