"Дифференцирование" вращения пространства

[B@R5uk]

Пусть есть n-мерное пространство. Вращение этого пространства вокруг начала координат на некоторый произвольный угол в некоторой плоскости можно описать линейным преобразованием R:

$$y=Rx,\qquad\qquad R\in\mathbb{R}^{n\times n},\qquad\qquad x,\;y\in\mathbb{R}^n$$

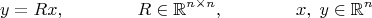
Важно отметить, что в отличие от трёхмерного, в многомерном пространстве вращение задаётся не осью вращения и углом, а плоскостью, в которой происходит вращение, и углом. Компоненты всех векторов пространства, которые находятся в плоскости поворачиваются, а компоненты, которые ортогональны этой плоскости, остаются неизменными. Если плоскость задана двумя единичными векторами

$$\lVert u\rVert=\lVert v\rVert=1$$

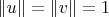
с углом β между ними равным углу поворота

$$\cos\beta=u^Tv$$

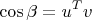
так, что при повороте вектор u переходит в вектор v то матрицу поворота можно выразить как

$$R\bigl(u,v\bigr)=I-\frac{2(u+v)(u+v)^T}{\lVert u+v\rVert^2}+2vu^T=I-\frac{(u+v)(u+v)^T}{1+u^Tv}+2vu^T$$

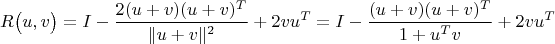
Здесь I — единичная матрица. Вывод этой формулы заключается в последовательном применении двух отражений Хаусхолдера ко всему пространству, что даёт поворот. Подробности в этом треде на MSE. Надо заметить, что выбор единичных векторов u и v при заданных плоскости и угле неоднозначен.

Если же плоскость поворота задавать двумя ортонормированными векторами в ней:

$$\lVert x\rVert=\lVert y\rVert=1,\qquad\qquad x^Ty=0$$

и углом поворота β в направлении от вектора x к вектору y, то матрица поворота запишется как

$$R\bigl(x,y,\beta\bigr)=I+\bigl(\cos\beta-1\bigr)\left(xx^T+yy^T\right)+\sin\beta\left(yx^T-xy^T\right)$$

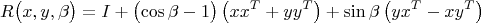
Эта формула складывается из трёх ортогональных компонент:

$$I-xx^T-yy^T$$

$$(x\cos\beat+y\sin\beta)x^T$$

$$(-x\sin\beta+y\cos\beta)y^T$$

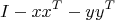
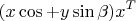
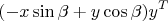
Первое слагаемое является ортогональным проектором на подпространство, являющимся ортогональным дополнением к плоскости вращения. Второе и третье слагаемые вращают компоненты вдоль векторов x и y, соответственно.

Цитата:

Теперь перехожу, собственно, к вопросу. Пусть у меня есть какая-то матрица поворота R. Если я её применю к пространству, то она сразу даст мне результат. Я же хочу посмотреть на движение пространства в процессе непрерывного поворота от начального положения к конечному. Это движение должно описываться чем-то, что является аналогом скорости для координаты, то есть некоторой дифференциальной величиной. Вопрос: как это правильно сделать?

Я так подозреваю, что произвольно заданную мне матрицу вращения R можно представить как последовательность бесконечно малых поворотов:

$$R\bigl(\beta\bigr)=\lim\limits_{N\to\infty}R^N\left(\frac{\beta}{N}\right)$$

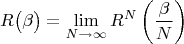
тогда один такой инфинитезимальный поворот можно разложить в виде

$$R(d\beta)=I+Sd\beta+O\left(d\beta^2\right)$$

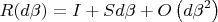
где антисимметричная матрица S — это и есть некий аналог скорости, своего рода "производная" матрицы вращения R. Я в правильном направлении двигаюсь?

[B@R5uk]

Может, кто-нибудь литературу посоветует какую-нибудь почитать по этому вопросу? Буду очень благодарен любой помощи.

[dgwuqtj]

Чтобы дифференцировать, надо вложить $R$ в какой-то путь внутри группы движений. Самый простой выбор — взять т.н. однопараметрическую подгруппу, у неё и хорошее дифференциальные уравнение, и вообще они очень просто устроены.

Вообще через одну точку группы Ли (ваше движение) может проходить много однопараметрических подгрупп. Скажем, все такие подгруппы содержат тождественное движение. Раз уж у вас $R$ является вращением в плоскости, то и группу стоит брать из вращений в ней же, т.е. $R(t) = \bigl( \begin{smallmatrix} \cos \omega t & - \sin \omega t \\ \sin \omega t & \cos \omega t \end{smallmatrix} \bigr)$ в ортонормированном базисе в плоскости, ну а на ортогональном дополнении эти операторы действуют тождественно. Параметр $\omega$ можно выбирать произвольно. Даже если вы захотите, чтобы при $t = 1$ было ваше исходное движение $R$, есть счётное количество выборов $ \omega$.

Если $R$ — поворот на угол $0 < \alpha < \pi$, то имеет смысл взять $\omega = 1$ и ориентацию так, чтобы $R$ получалось при $t = \alpha$. А при $\alpha = \pi$ уже есть два выбора ориентации, т.е. можно вращать или по часовой стрелке, или против, и нет предпочтительного выбора.

[B@R5uk]

Мммм... В групповых терминах применительно к вращению пространства я не очень разбираюсь. В частности я так и не дошёл до того, что такое группы Ли и с чем их едят, когда с группами конечного игрался. dgwuqtj, посоветуйте, пожалуйста, какую-нибудь литературу про них легкую для понимания. В вики довольно обширный список из очень объёмных книг. Спасибо за комментарий!

[dgwuqtj]

Есть относительно небольшая книжка Адамс, Лекции по группам Ли. Экспоненциальное отображение и однопараметрические подгруппы там где-то в начале.

Если коротко, то речь идёт об отображениях специального вида $R \colon t \mapsto \exp(t X) = \sum_{k = 0}^\infty \frac {t^k X^k} {k!}$, где $X$ кососимметрическая матрица (у вас же группа $\mathrm{SO}(n)$). Это гомоморфизм групп, поэтому и называется "однопараметрической подгруппой".

[B@R5uk]

dgwuqtj, там в сумме в знаменателе k факториал, а не ноль? Если да, то это легко суммируется, если воспользоваться спектральным разложением для матрицы X (оно существует?):

$$X=Q\Lambda Q^*$$

$$\exp\bigl(tX\bigr)=Q\operatorname{diag}\Bigl(\exp\bigl(t\operatorname{diag}(\Lambda)\bigr)\Bigr)Q^*$$

Где diag — это взятие главной диагонали, если аргумент есть квадратная матрица, или построение диагональной матрицы, если аргумент — вектор. Сейчас помедитирую над этим, может чего выйдет методом исключительно матричной теории.

[dgwuqtj]

B@R5uk
Да, там опечатка, исправил знаменатели. Из этой формулы и вылезает тригонометрия.

[B@R5uk]

Ну, хорошо. Если взять формулу выше для матрицы вращения

$$R\bigl(\beta\bigr)=I+\bigl(\cos\beta-1\bigr)\left(xx^T+yy^T\right)+\sin\beta\left(yx^T-xy^T\right)$$

то непосредственным вычислением можно убедиться, что

$$R\bigl(\beta\bigr)=I-xx^T-yy^T+\bigl(x,\;y\bigr)\left(\begin{array}{rr}\cos\beta&\sin\beta\\-\sin\beta&\cos\beta\end{array}\right)\bigl(x,\;y\bigr)^T$$

Здесь первые три слагаемые образуют ортогональный проектор на ортогональное дополнение к плоскости вращения. Если в этом подпространстве задать ортонормированный базис и из координат векторов этого базиса сформировать матрицу B, то формулу можно дальше преобразовать так:

$$R\bigl(\beta\bigr)=BB^T+\bigl(x,\;y\bigr)\left(\begin{array}{rr}\cos\beta&\sin\beta\\-\sin\beta&\cos\beta\end{array}\right)\bigl(x,\;y\bigr)^T,\qquad\qquad B\in\mathbb{R}^{n\times(n-2)}$$

$$B^TB=I_{n-2},\qquad\qquad B^T\bigl(x,\;y\bigr)=0$$

Отсюда видно следующее разложение для матрицы вращения R:

$$R\bigl(\beta\bigr)=A\left(\begin{array}{rrr}\cos\beta&\sin\beta&0\\-\sin\beta&\cos\beta&0\\0&0&I_{n-2}\end{array}\right)A^T=AG_{2,1}\bigl(\beta\bigr)A^T,\qquad\qquad A=\bigl(x,\;y,\;B\bigr)\in\mathbb{R}^{n\times n}$$

$$AA^T=A^TA=I$$

где G — матрица вращения Гивенса. Это уже почти что спектральное разложение. Надо только вспомнить, что матрица простого поворота имеет пару комплексно сопряжённых собственных значений. Сделаем замену:

$$z=\frac{c(x+iy)}{\sqrt{2}},\qquad w=\frac{d(x-iy)}{\sqrt{2}},\qquad\lvert c\rvert=\lvert d\rvert=1$$

Здесь c и d — произвольные комплексные числа на единичной окружности (их наличие соответствует неоднозначности в выборе векторов x и y). Поскольку столбцы x и y ортогональны друг другу и столбцам матрицы B, то же самое верно и для комплексных столбцов z и w (они так же нормированы на единицу, именно для этого корни из 2 в знаменателях выше):

$$\bigl(z,\;w\bigr)^\ast\bigl(z,\;w\bigr)=I,\qquad\qquad B^T\bigl(z,\;w\bigr)=0$$

Непосредственным вычислением можно убедиться, что

$$R\bigl(\beta\bigr)=BB^T+\bigl(z,\;w\bigr)\left(\begin{array}{ll}e^{i\beta}&0\\0&e^{-i\beta}\end{array}\right)\bigl(z,\;w\bigr)^\ast$$

Получается, что в базисе столбцов матрицы Q:

$$Q=\bigl(z,\;w,\;B\bigr),\qquad\qquad QQ^\ast=Q^\ast Q=I$$

матрица вращения R диагонализируется:

$$R\bigl(\beta\bigr)=Q\operatorname{diag}\bigl(e^{i\beta},\;e^{-i\beta},\;\underbrace{1,\;\ldots,\;1}_{n-2\text{ раза}}\;\bigr)Q^\ast$$

Получилось спектральное разложение R. Таким образом, если задана произвольная матрица R вращения пространства, то можно посчитать её сингулярное разложение и проделать преобразования выше в обратном порядке, что позволит найти координаты векторов, задающих плоскость вращения и угол, на который это вращение происходит.

-- 26.01.2026, 12:04 --

Выходит, что моя матрица S, "производная" матрицы поворота R — это на самом деле матричный логарифм матрицы R:

$$R=Q\Lambda Q^\ast,\qquad\qquad S=\ln\bigl(R\bigr)=Q\ln\bigl(\Lambda\bigr)Q^\ast$$

где логарифм в самом правом выражении берётся только у диагональных элементов диагональной матрицы Λ (диагональные единицы при этом обратятся в нули, поэтому ранг матрицы S может оказаться меньше размерности пространства n). Результат даже получается действительным (так как логарифм от пары комплексно сопряжённых чисел является парой комплексно сопряжённых чисел).

[пианист]

B@R5uk
А что, собс-но, Вы хотите получить?