Сечения Дедекинда и причинно-следственная связь

[cxzbsdhwert]

Дедеки́ндово сече́ние — один из способов построения вещественных чисел из рациональных (скопировал с Википедии).

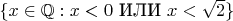
Например, корень из двух определяется как пара множеств $\{x\in\mathbb Q:x<0\text{ ИЛИ }x<\sqrt{2}\}$ (почему ещё отдельно условие меньше нуля?) и его дополнение до $\mathbb Q$.

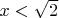
Как мы задали условие $x<\sqrt{2}$, если корня из двух на этом этапе нет? Мы же занимаемся тем, что его определяем

(Оффтоп)

Наверное никто не ответит на этот вопрос лучше, чем пользователь с псевдонимом Dedekind

[mihaild]

cxzbsdhwert в сообщении #1715544 писал(а):

Например, корень из двух определяется как пара множеств $\{x\in\mathbb Q:x<0\text{ ИЛИ }x<\sqrt{2}\}$ (почему ещё отдельно условие меньше нуля?)

Потому что написано неправильно. Откуда эта формулировка? В википедии я сейчас такой не вижу.
Правильно так: $\{x \in \mathbb Q | x < 0 \vee \textcolor{blue}{x^2 < 2}\}$.

[Dedekind]

cxzbsdhwert
Обычно пишут $\{x\in\mathbb Q:x<0\text{ ИЛИ }x^2<2\}$

[cxzbsdhwert]

mihaild
Извините, не внимательно посмотрел. Тут можно удалять свои тупые вопросы, чтобы не засорять форум?

[Dedekind]

(Оффтоп)

cxzbsdhwert в сообщении #1715544 писал(а):

Наверное никто не ответит на этот вопрос лучше, чем пользователь с псевдонимом Dedekind

Эх, опоздал:)