Каноническое представление и замена переменных

[Alexander_1]

Дорогие форумчане!

У меня есть два малых параметра: $\varepsilon, x$, и есть выражение

$$\varepsilon x + x^2 + x^3.$$

Цель - привести его к как можно более простому виду. Этот вид такой:

$$\sigma y + y^2,$$

где $\sigma$ "заменяет" $\varepsilon$, а $y$ "заменяет" $x.$

Ища $y, \sigma$в виде рядов по степеням $\varepsilon$, то есть

$$y = y(x;\varepsilon) = g_0(x) + \varepsilon g_1(x)\varepsiolon + \varepsilon g_2(x)\varepsiolon^2 + \varepsilon g_3(x)\varepsiolon^3 + \ldots$$

$$\sigma = \varepsilon + p_1 \varepsilon + p_2 \varepsilon^2 + p_3 \varepsilon^3 + \ldots, $$

и подставляя в выражение

$$\begin{equation}\label{eq}\varepsilon x + x^2 + x^3 = \sigma y + y^2,\end{equation}$$

найдем последовательно все составляющие, то есть все коэффициенты $p_j$ и все функции $g_j(x).$

Вопрос, как доказать что такая замена существует, то есть что ряд сходится.

[nnosipov]

Alexander_1
Положите, например, $\sigma=\varepsilon$ и решите уравнение $\varepsilon x+x^2+x^3=\varepsilon y+y^2$ относительно $y$. Будем Вам сразу явно заданная функция $y=y(x)$, которую, если нужно, можно и в ряд разложить в окрестности $x=0$.

[Евгений Машеров]

Если он "малый", то, может, просто отбросить кубический член?

[dsge]

Подставьте в формулу (1) $y$ и $\sigma$ из формул выше. Соберите справа все слагаемые, содержащие $\varepsilon$, приравняйте их конффициент к $x$, получите
$g_0(1+2g_1)=x$.
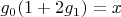
Дальше соберите справа все члены без $\varepsilon$, найдите $g_0$. Подставьте это в предыдущее уравнение, найдёте $g_1$.
Все остальные $g_i$ и $p$ будут равны нулю, поэтому ряды сходятся.
Чтобы учесть малость $x$, надо некоторые радикалы разложить в ряд Тейлора.