На первый взгляд линейно комбинируя
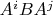
можно получить

.
Да, я тоже так подумал. Распишу для

, чтобы лучше увидеть обратимость получающейся матрицы. Буду считать, что
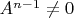
, иначе переходим к меньшему значению

.
Из исходного уравнения получаем систему

уравнений, умножая исходное уравнение, то слева, то справа на

:
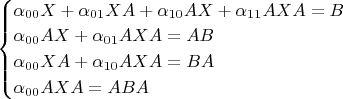
Если переменные это
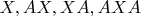
, то обратимость матрицы системы очевидна, так как матрица имеет вид
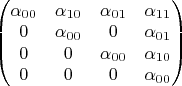
.
Если

, то принцип тот же: получаем

уравнений. В каждом уравнении будет присутствовать ненулевой элемент поля
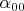
. Причём, в различных уравнениях он будет коэффициентом при различных матрицах вида
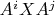
, которые мы пронумеруем в качестве неизвестных
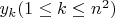
так, чтобы матрица системы была треугольная с детерминантом равным
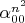
. Такая нумерация для того, чтобы показать разрешимость системы.