Альтернативное определение второй производной

[Dedekind]

Задача: пусть $f$ дважды дифференцируема на открытом интервале $A$, содержащем $a$ и $f''$ непрерывна в $a$. Покажите, что

$$\lim_{h\to 0}\dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2}$$

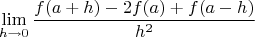
Примечание: до этого было доказано, что если функция $g$ дифференцируема в точке $c$ открытого интервала, то

$$g'(c) = \lim_{h\to 0}\dfrac{g(c+h) - g(c-h)}{2h}$$

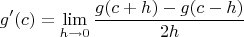
Я решил, применив правило Лопиталя, но есть сомнения, так как вроде бы нигде не используется непрерывность второй производной.
Функция $f$ непрерывна и дифференцируема на $A$, а также в точке $h = 0$ числитель и знаменатель равны нулю. Также (взял производные по $h$ от числителя и знаменателя):

$$\lim_{h\to 0} \dfrac{f'(a+h) - f'(a-h)}{2h} = f''(a)$$

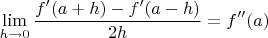
по примечанию.
Следовательно, по правилу Лопиталя

$$\lim_{h\to 0}\dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2} = \lim_{h\to 0} \dfrac{f'(a+h) - f'(a-h)}{2h} = f''(a)$$

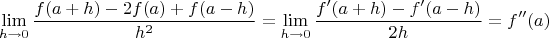
Где ошибка?

[mihaild]

Всё правильно. То же самое можно получить из формулы Тейлора в форме Пеано: $f(a + h) = f(a) + f'(a) \cdot h + f''(a) / 2 \cdot h + o(h^2)$.

[Dedekind]

mihaild
Спасибо!