зависимость решения системы диф уравнений от параметра

[IrinaZub]

Здравствуйте!

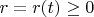
Рассмотрим следующую систему дифференциальных уравнений на функции $r=r(t)\geq 0$ и $\varphi=\varphi(t)$, зависящую от параметра $a$:

$$\dot{r}^2=\frac{(2-5r)P(r)}{r^2(2-(5+a)r)^2},\quad P(r)=2r(2-(5+a)r)^2-(2-5r),\quad \dot{\varphi}=\frac{2-5r}{r^2(2-(5+a)r)}.$$

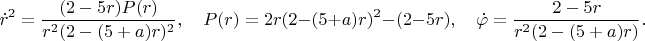
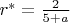
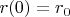
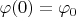
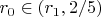
Считаем, что модуль параметра $a$ достаточно мал. Тогда правая часть первого уравнения системы неотрицательна на некотором отрезке $[r_1,2/5]$, лежащем левее точки сингулярности $r^{\ast}=\frac{2}{5+a}$ при $a<0$ и правее этой точки при $a>0$. Выберем подходящие начальные данные $r(0)=r_0$, $\varphi(0)=\varphi_0$ так, чтобы $r_0\in (r_1,2/5)$. 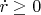Разрешим первое уравнение системы относительно $\dot{r}$, считая, что $\dot{r}\geq 0$, и найдем решение этой задачи Коши. Существует конечный момент времени $t_1>0$ такой, что $r(t_1)=2/5$, $\varphi(t_1):=\varphi_1$. 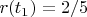Дальше мы рассмотрим задачу Коши, считая, что $\dot{r}$ неположительна, с начальными данными $r(t_1)=2/5$, $\varphi(t_1)=\varphi_1$. 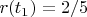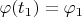За конечный промежуток времени $t_2>t_1$ мы имеем $r(t_2)=r_1$, $\varphi(t_2):=\varphi_2$. 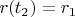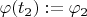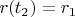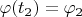Дальше снова рассмотрим задачу Коши, считая, что $\dot{r}$ неотрицательна, с начальными данными $r(t_2)=r_1$, $\varphi(t_2)=\varphi_2$ и т.д. Получаем, что функция $r(t)$ совершает колебание на отрезке $[r_1,2/5]$.

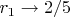
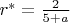
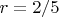
При стремлении параметра $a$ к нулю область движения функции $r(t)$ - отрезок $[r_1,2/5]$ - стягивается в точку $2/5$ (то есть $r_1\rightarrow 2/5$ при $a\rightarrow 0$), при этом и точка сингулярности $r^{\ast}=\frac{2}{5+a}$ стремится к $r=2/5$. Меня интересует, как ведет себя кривая $\varphi=\varphi(r)$ при $a\rightarrow 0$.

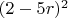
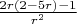
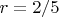
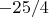
Меня смущает, что при $a=0$ после сокращения числителя и знаменателя на $(2-5r)^2$ правая часть первого уравнения системы равна $\frac{2r(2-5r)-1}{r^2}$, и при $r=2/5$ она равна $-25/4$, то есть отрицательна.

Спасибо!