Доброго времени суток.
Есть такая формула Андреотти-Норге. Это интегральное представление для производной голоморфной функции нескольких переменных. Привожу её по книге Айзенберга и Южакова "Интегральные представления и вычеты в многомерном комплексном анализе":
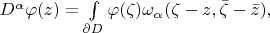
![$\omega_\alpha(f,w)=\frac{(n-1)!\alpha!}{(2\pi i)^n}\frac{1}{\langle w,f^{(\alpha+I)}\rangle^n}\sum\limits_{k=1}^n(-1)^{k-1}w_k^{\alpha_k+1}dw_{[k]}^{(\alpha+I)}\wedge df,$ $\omega_\alpha(f,w)=\frac{(n-1)!\alpha!}{(2\pi i)^n}\frac{1}{\langle w,f^{(\alpha+I)}\rangle^n}\sum\limits_{k=1}^n(-1)^{k-1}w_k^{\alpha_k+1}dw_{[k]}^{(\alpha+I)}\wedge df,$](https://dxdy-03.korotkov.co.uk/f/2/9/8/2982874480dfdac37c451fbcc7d8036a82.png)
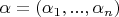
- мультииндекс,
![$dw_{[k]}$ $dw_{[k]}$](https://dxdy-01.korotkov.co.uk/f/0/e/f/0efa35fd21b88c890bdff17569ead49a82.png)
- значит

-й дифференциал пропущен. Я не могу даже начать осмысление этой формулы, потому что до конца её не понимаю. Как понимать степень
![$dw_{[k]}^{(\alpha+I)}$ $dw_{[k]}^{(\alpha+I)}$](https://dxdy-03.korotkov.co.uk/f/6/0/e/60e487689e1c54873fee547dd4b402c182.png)
? Это что, степени дифференциальных форм? Так ведь внешнее произведение 1-формы на себя - это нуль. Или это и не степень вовсе, но что тогда?
Нигде не нашёл внятного объяснения. Наверное плохо искал. И спрашивал уже людей. В лучшем случае сказали, что у меня ошибка в записи. Но это мне сомнительно, потому что и в других местах то же написано.