Квадрокоптер. Ньютон-Эйлер не равен Эйлеру-Лагранжу

[Zahar Kartashov]

В [1] двумя способами получают уравнения движения для квадрокоптера: напрямую через уравнения Ньютона-Эйлера и косвенно по методу Эйлера-Лагранжа. Меня в данном случае интересуют уравнения для вращательных степеней свободы. Если сравнить уравнения для углов Эйлера, полученные по методу Ньютона-Эйлера и уравнения для углов Эйлера, полученные по методу Эйлера-Лагранжа, то видно, что они отличаются. Причем, этот результат не только в этой статье втречается, те же самые формулы приводятся в массе статей и видеолекций на Youtube (напр. https://www.youtube.com/watch?v=xCoFaTyn5dg).

Краткая выдержка из [1]:

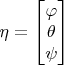
$\eta=\begin{bmatrix} \varphi \\ \theta \\ \psi \end{bmatrix}$ - углы Эйлера (по порядку - крена, тангажа, рыскания)

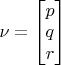
$\nu=\begin{bmatrix} p \\ q \\ r \end{bmatrix}$ - вектор угловой скорости квадрокоптера в связанной системе координат (body frame)

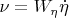
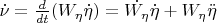
$\nu = W_\eta \dot{\eta}$ - связь угловых скоростей в связанной системе координат с углами Эйлера ((4) в [1]). Соответственно $\dot{\nu} = \frac{d}{dt}(W_\eta \dot{\eta})=\dot{W_\eta} \dot{\eta} + W_\eta \ddot{\eta}$. И вот если мы теперь подставим эти два выражения в уравнение Эйлера ниже, то мы получим уравнение вращательного движения относительно углов Эйлера.

Уравнение Эйлера (для вращательных степеней свободы) в связанной системе координат (body frame) ((11) в [1]):
$\boldsymbol{I} \dot{\nu }+ \nu \times (\boldsymbol{I} \nu) + \boldsymbol{\Gamma}= \boldsymbol{\tau}$

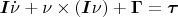
И далее там приводится уравнение для вращательных степеней свободы ((18) в [1]), полученное по методу Эйлера-Лагранжа:
$\boldsymbol{J} \ddot{\eta}+ \boldsymbol{C}(\eta, \dot{\eta}) \dot{\eta}= \boldsymbol{\tau}$

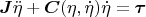
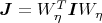
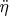
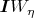
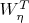
И тут $\boldsymbol{J} = W_\eta^T \boldsymbol{I} W_\eta$, а в уравнении Эйлера член при $\ddot{\eta}$ равен $\boldsymbol{I} W_\eta$, т.е. они не совпадают (отличаются на матричный множитель $W_\eta^T$ слева).

Вопрос: В чем тут дело? Это ошибка? Если не ошибка, то эквивалентные все же это уравнения или нет?

1. https://sal.aalto.fi/publications/pdf-files/eluu11_public.pdf