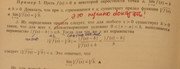Пределы. Интервал и соотношение

[Pavel_Kotoff]

Друзья, конечно, я не специалист, но тем не менее. Начнём. Из простецкого определения предела выходит, что некой точке в горизонтальной окресности точки с абсциссой а $\[\left] {a - \delta ;a + \delta } \right[\]$ (это симметричный интервал) соответствует определённая точка из вертикальной окресности точки с ординатой b (сим. интервал). Именно это и означает, что при х стремится к а, y стремится к b, т.е., b есть предел функции f(x), если абсцисса приближается к а. И вертикальная и горизонтальная окресности (интервалы) это отрезки. Или я неправ?
$\[\mathop {\lim }\limits_{x \to a} f(x) = b\] $ если $\[\left| {f(x) - b} \right| < \varepsilon \] $ при $\[\left| {x - a} \right| < \delta \]; x≠a

Тогда мне становится непонятна задача 3 из учебника А.Д. Кутасова «Пособие по математике для поступающих в вузы» М:. Наука 1985. Стр.94
«Есть предел $\[\mathop {\lim }\limits_{x \to a} f(x) = b\] $ для f(x)>0 в некоторой окресности точки а. Докажите, что при тех же условиях $\[\mathop {\lim }\limits_{x \to a} \sqrt {f(x} ) = \sqrt b \]$
Из определения предела следует , что (sic!) $\[\left| {f(x) - b} \right| > \varepsilon /b\]$ »
Простите, но в левой части ЧИСЛО, а в правой ОТНОШЕНИЕ, и как они это неравенство вообще вывели, кто мне подскажет?
Дальше тоже интересно:
«$\[\left| {\sqrt {f(x)} - \sqrt b } \right| = \frac{{\left| {f(x) - b} \right|}}{{\sqrt {f(x)} + b}} < \frac{\varepsilon }{b} = \frac{{\left| {f(x) - b} \right|}}{b}\]$ ».
Ясно почему неравенство такое, слева у дроби при том же числителе знаменатель больше, но откуда$ \[\left| {\sqrt {f(x)} - \sqrt b } \right| = \frac{{\left| {f(x) - b} \right|}}{{\sqrt {f(x)} + b}}\]$ ?
Если так, то: $\[\left| {\sqrt {f(x)} - \sqrt b } \right| = \frac{{\left| {\sqrt {f(x)} - \sqrt b } \right|\cdot \left| {\sqrt {f(x)} + \sqrt b } \right|}}{{\sqrt {f(x)} + \sqrt b }} = \frac{{\left| {f(x) - b} \right|}}{{\sqrt {f(x)} + \sqrt b }}\]$
Короче, я в замешательстве. Скрины прилагаются.

[Combat Zone]

Там две опечатки. Вот это место:

Pavel_Kotoff в сообщении #1714083 писал(а):

Из определения предела следует , что (sic!) $\[\left| {f(x) - b} \right| > \varepsilon /b\]$ »

следует читать так:
Из определения предела следует , что [...] \[\left| {f(x) - b} \right| < \varepsilon b\]$.
Далее без изменений.

-- 06.01.2026, 04:15 --

Pavel_Kotoff в сообщении #1714083 писал(а):

но откуда$ \[\left| {\sqrt {f(x)} - \sqrt b } \right| = \frac{{\left| {f(x) - b} \right|}}{{\sqrt {f(x)} + b}}\]$ ?

а это стандарт. Домножили на сопряженное, разделили на него же.

[nnosipov]

Pavel_Kotoff в сообщении #1714083 писал(а):

но откуда$ \[\left| {\sqrt {f(x)} - \sqrt b } \right| = \frac{{\left| {f(x) - b} \right|}}{{\sqrt {f(x)} + b}}\]$ ?

Тоже опечатка: в знаменателе должно быть $\sqrt{f(x)}+\sqrt{b}$.

[Pavel_Kotoff]

Добрый день! Спасибо. По-моему, две опечатки на такой маленький пример это многовато. За это морду бить надо, как говорил Остап Бендер. Я ж это неравенство уже доказывать стал, грешным делом. Чуть крыша не съехала.)
Кстати, с опечатками я уже встречался в учебнике Колмогорова "Алгебра для старших классов" и ещё где-то.

[nnosipov]

Pavel_Kotoff в сообщении #1714083 писал(а):

из учебника А.Д. Кутасова «Пособие по математике для поступающих в вузы» М:. Наука 1985.

О, как забавно: именно по этой книжке я готовился, когда поступал на мехмат (только издание более раннее у меня было). Возможно, тоже натыкался там на опечатки, но уже не помню.

[Combat Zone]

nnosipov в сообщении #1714114 писал(а):

Тоже опечатка: в знаменателе должно быть $\sqrt{f(x)}+\sqrt{b}$.

А, да. По ночам я образец концентрации внимания )

Combat Zone в сообщении #1714112 писал(а):

Из определения предела следует , что [...] $\left| {f(x) - b} \right| < \varepsilon b$.

Тогда тут справа надо делать ${} < \varepsilon \sqrt b$. Но это, по большому счету, не имеет значения.

Pavel_Kotoff в сообщении #1714118 писал(а):

По-моему, две опечатки на такой маленький пример это многовато.

Соглашусь, многовато. Зато у вас был повод зарегистрироваться.

[Pavel_Kotoff]

Если откровенно, у меня были свои топики на mathhelpplanet, но форум почему-то умер, не пойму, что случилось, вот и пришлось идти сюда.) Надеюсь, что эта платформа не хуже.

[Pavel_Kotoff]

nnosipov в сообщении #1714121 писал(а):

Pavel_Kotoff в сообщении #1714083 писал(а):

из учебника А.Д. Кутасова «Пособие по математике для поступающих в вузы» М:. Наука 1985.

О, как забавно: именно по этой книжке я готовился, когда поступал на мехмат

А я когда готовился поступать в свой вуз 25 лет назад, то на Кушнира налегал. Но там подобных злостных опечаток, вроде, не замечал. Так давно это было, почти как в прошлой жизни.)

[nnosipov]

Pavel_Kotoff в сообщении #1714142 писал(а):

на Кушнира налегал

У Кушнира в его "Шедеврах школьной математики" шедевральные ошибки встречаются, когда он пытается "легко" решать сложные задачи по элементарной теории чисел. Но, насколько я понимаю, это не его основной профиль, он вроде бы по геометрии специализировался.

Или это какой-то другой Кушнир?

[Pavel_Kotoff]

Нет, это именно тот самый Кушнир. Ещё Сканави был популярен.