Дурацкий вопрос

[waxtep]

Наверное, это сюда. Возможен ли при игре в подкидного дурака втроем такой расклад, что игра не закончится никогда?
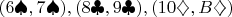
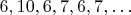
На первый взгляд, - да: пусть $30$ карт уже выбыло, а на руках у каждого по две карты одной некозырной масти, при этом достоинства всех карт разные, например, $(6\spadesuit,7\spadesuit), (8\clubsuit, 9\clubsuit), (10\diamondsuit, B\diamondsuit)$, при козыре черви. Пусть ходит первый игрок, и пусть каждый из игроков ходит с карты наименьшего достоинства, тогда ходы будут $6,10,6,7,6,7,\ldots$ до бесконечности. Вообще говоря, это не форсированно: при другой стратегии игра с таким раскладом может и закончиться, если, например, третий игрок отдаст сначала вальта, а потом сунет под него десятку (и это даже разумно: если первый игрок не отдаст этого вальта по глупости, то форсированно проигрывает второй игрок; игра в подкидного втроем так же глубока и неисчерпаема, как атом).

И, собственно, вопрос: может ли такой (или иной, имеющий тенденцию к зацикливанию) расклад реально возникнуть в игре? В идеале вообще форсированно циклящий при лучшей игре всех троих (приведенный выше расклад не таков), но хотя бы без явной кооперации игроков, и может быть при неидеальной игре одного из них, или иных дополнительных ограничениях. С ходу не соображу, а симулировать на всех $36$ бумажных картах пока ленюсь.