У меня есть предположение, что для морфизмов
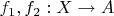
вводится отношение
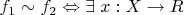
такой, что
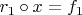
и
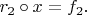
Там ровно это и написано, только в виде формулы. Ну и

— это просто какое-то бинарное отношение, странно обозначать его значком

, используемым для отношений эквивалентности.
Давайте для простоты считать, что

имеет все конечные пределы, тогда
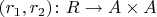
будет мономорфизмом. Рассмотрим вложение Йонеды
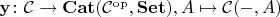
. Оно замечательно тем, что является вполне строгим функтором, а также сохраняет конечные пределы и мономорфизмы. Мономорфизм
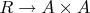
переходит в семейство инъективных отображений
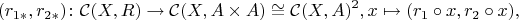
естественных по

. Ну а

— это в точности образ
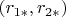
.
Кстати, регулярные категории тут пока ни при чём.