Всегда ли возможно оставить по одной фигуре на линии?

[gipokrat]

На одном из занятий математического кружка для 5-го класса предлагалась следующая задача:

На шахматной доске расставлены фигуры так, что на каждой горизонтали и вертикали стоит не меньше двух фигур. Всегда ли можно снять с доски несколько фигур так, чтобы на каждой горизонтали и вертикали осталось ровно по одной фигуре?

(Источник задачи: здесь (задача №10).

Мой контрпример:

\begin{array}{c|c|c|c|c|c|c|c|c|} \hline 8&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet\\ \hline 7&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 6&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 5&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 4&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 3&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 2&\bullet&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\phantom{\bullet}&\bullet\\ \hline 1&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet&\bullet\\ \hline &\mathrm a&\mathrm b&\mathrm c&\mathrm d&\mathrm e&\mathrm f&\mathrm g&\mathrm h\\ \hline \end{array}

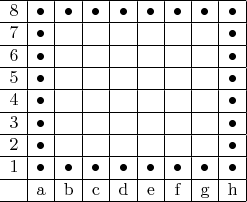
А вот контрпример, который предложил Искусственный Интеллект:

ChatGPT писал(а):

Нет, не всегда.

**Контрпример (для обычной доски 8×8):**
Поставим фигуры так:

* на всех клетках прямоугольника **5×4** в левом верхнем углу (1–5-я горизонтали и 1–4-я вертикали);
* на всех клетках прямоугольника **3×4** в правом нижнем углу (6–8-я горизонтали и 5–8-я вертикали).

Тогда:

* в каждой горизонтали стоит **4** фигуры (≥2);
* в вертикалях 1–4 стоит **5** фигур, в вертикалях 5–8 стоит **3** фигуры (везде ≥2).

Но сделать так, чтобы осталось **ровно по одной** в каждой горизонтали и вертикали, нельзя:
в вертикалях **5–8** фигуры встречаются **только** на горизонталях **6–8** (то есть всего в **трёх** строках). А вертикалей 5–8 **четыре**, значит выбрать по одной фигуре в каждой из этих 4 вертикалей так, чтобы они лежали в разных горизонталях, невозможно (не хватает “разных” строк).

Следовательно, условие “не меньше двух на каждой горизонтали и вертикали” **не гарантирует** такой отбор.

Как мы видим, в ИИ-шном примере используются 32 фигуры, а в моём всего 28.

А каким наименьшим числом фигур можно обойтись?
И как доказать, что оно действительно наименьшее?
Пожалуйста, помогите решить.
Заранее благодарю!

[Null]

$$ \begin{tabular}{|l|l|l|l|l|l|l|l|} \hline \bullet &\bullet & & & & & & \\ \hline \bullet &\bullet & & & & & & \\ \hline \bullet &\bullet & & & & & & \\ \hline & &\bullet & & & & &\bullet \\ \hline & & \bullet &\bullet & & & & \\ \hline & & &\bullet &\bullet & & & \\ \hline & & & &\bullet &\bullet &\bullet & \\ \hline & & & & &\bullet &\bullet &\bullet \\ \hline \end{tabular} $$

По лемме Холла паросочетания не будет если существует $k$ строк, таких что, фигуры в них занимают $l<k$ столбцов. Это подсказка.

[wrest]

gipokrat в сообщении #1713951 писал(а):

Как мы видим, в ИИ-шном примере используются 32 фигуры, а в моём всего 28.

Можно убрать угловые, останется 24. Ну и вообще, провести две любые вертикальные и две любые горизонтальные линии, убрать пересечения, останется 24.

-- 03.01.2026, 13:06 --

gipokrat в сообщении #1713951 писал(а):

Как мы видим, в ИИ-шном примере

Слабый ИИ или негодный промпт :)
Мне qwen выдал расстановку на $2n+2=18$ фишек. С леммой Холла и прочим блекджеком (двудольные графы, в общем всё для 5-го класса). Но, правда, я и просил его минимальную а не любую.

[wrest]

В терминах теоремы о свадьбах, задача выглядит примерно так. Есть 8 мальчиков и 8 девочек, каждый мальчик помолвлен на не менее чем 2 девочках, а каждая девочка на не менее чем 2 мальчиках. Каково минимальное количество помолвок такое, что можно расторгнуть их часть, и при этом все поженятся не оставив нереализованных помолвок. Тоже для 5-го класса норм

[wrest]

wrest в сообщении #1713961 писал(а):

и при этом все поженятся

В смысле НЕ все, конечно. Ну, вы поняли...