Разумное док-во фальшивого разложения и самого определителя

[cxzbsdhwert]

Я бы хотел узнать есть ли более подробное доказательство равенства нулю фальшивого разложения. Подчеркну - хотел бы узнать есть ли, а не само доказательство, если оно есть. Если его нет, то по крайней мере сейчас нет желания пытаться его изобрести. Если есть, то конечно подумаю.

Я ознакомился уже с четырьмя разными источниками и у них у всех одно и тоже не удовлетворяющее меня доказательство верности вышеуказанного утверждения:
1. Исходя из того факта, что при разложении определителя матрицы $A$ порядка $n$ по строке, значения строки не учитываются в алгебраических дополнениях, выступающих в качестве множителей в каждом из $n$ слагаемых, рассматривая фальшивое разложение по строке $i$, можно заменить элементы несовпадающей строки $j$ на произвольные - значение алгебраического дополнения не изменится.
2. Изменить элементы в $j$-ой строке можно, в частности на те же, что у $i$-ой строки, по которой производится разложение.
3. Тогда определитель изменённой $A'$ с двумя одинаковыми строками на $i$-ом и на $j$-ом месте точно равен нулю по св-ву кососимметричености.
4. Хотя $A'$ отлична от $A$ матрица, выражение для "правильного" разложения по $j$ - строке всегда будет совпадать с интересующим фальшивым разложением по $i$ $A$, т.к. у них сходятся алгебраические дополнения, потому что у соответствующих миноров исключена одна и та же строка (и столбец) и сходятся сомножители дополнений, поскольку элементы $j$-ой строки $A'$ это элементы $i$-ой строки как $A'$ так и $A$.
5. Дальше делается заключение "ну значит вот такое разложение равно нулю".

Но после такого доказательства, понимания того, как всё-таки так получается, что слагаемые фальшивого разложения всегда дают ноль не прибавляется. Ведь важно заметить, что это происходит не потому что слагаемые нулевые, по крайней мере не в общем случае.
То есть каким-то образом получается так, что слагаемые фальшивого разложения будучи ненулевыми тем не менее всегда друг-друга компенсируют, и приведённые выше соображения никакого разумного объяснения этому не дают.
Вот я и хотел бы узнать, стоит ли за этим какая-то закономерность, кроме как "ну вот так получается по аксиоматическому определению определителя".

Вот как с аддитивностью и мультипликативностью определителя - определитель произведения матриц любых квадратных матриц выражается хорошей закономерностью $\det AB = \det A \det B$. Для определителя суммы такой формулы, насколько я знаю нет.
Не так ли и в случае с фальшивым разложением?

___
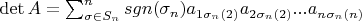
Ну и возможно что если более разумное объяснение есть, то оно основывается на разумном объяснении того как фактически так получается, что обычный определитель равен нулю если есть линейно-зависимые строки. Как так получается что $n!$ слагаемых из формулы $\det A=\sum_{\sigma \in S_n}^{n}{sgn(\sigma_n)a_{1\sigma_n(2)}a_{2\sigma_n(2)}...a_{n\sigma_n(n)}}$ не обязательно будучи нулевыми в сумме всегда будут равны нулю.
Всё объяснение которое было дано на лекциях - аксиоматично:
Определитель матрицы с л\з строками равен нулю, потому что по аксиоматическим свойствам определителя есть две пропорциональные строки (или эл.преоразованиями можно получить пропорциональные строки, а эл. преобр. не меняют свойства определителя быть равным или неравным нулю (по тем же аксиоматическим свойствам)), а значит по полилинейности из одной из них можно вынести коэффициент за знак определителя так чтобы строки были равны, ну а по кососимметричности постулируется (ну почти постулируется) что тогда определитель равен нулю.

Ещё раз подчеркну, что меня интересует не само объяснение, а есть ли оно. Стоит ли тратить время на его нахождение, или дающееся на лекции доказательства исчерпывающее и нужно двигаться дальше?

[nnosipov]

cxzbsdhwert в сообщении #1713824 писал(а):

или дающееся на лекции доказательства исчерпывающее и нужно двигаться дальше

Или.

[cxzbsdhwert]

nnosipov в сообщении #1713825 писал(а):

cxzbsdhwert в сообщении #1713824 писал(а):

или дающееся на лекции доказательства исчерпывающее и нужно двигаться дальше

Или.

Спасибо. Понимаю, что вопросы предполагающие ответ "да" или "нет" не приветствуются

[Anton_Peplov]

Anton_Peplov в сообщении #1529899 писал(а):

Грабли № 4. Погоня за ощущением естественности.
Ты пытаешься как следует понять доказательство теоремы и признаёшь своё понимание полноценным, только если у тебя возникло ощущение "ага, ну конечно, а разве могло быть иначе!". Если ты разобрал каждый шаг в доказательстве теоремы, согласился, что он сделан по правилам, но всё равно не ощутил своего "ага, ну разумеется!", ты считаешь, что тебе нужно ещё покопаться в теореме - часами, днями, неделями. Но правда в том, что ты гонишься за призраком. В математике много неожиданных, контринтуитивных, сложных для принятия вещей. И анекдот "в первый раз не понял, во второй не понял, в третий привык" - не такой уж и анекдот. Зачастую "понятное" - просто синоним "привычного". А может быть, глубокие причины, по которым всё устроено так, а не иначе, всё же существуют, но чтобы их понять, придётся изучить ещё несколько томов непростой математики. Так что гнаться за "ага, ну разумеется!" не следует. Если каждый шаг в доказательстве теоремы понят и признан законным, на этом следует остановиться, даже если это доказательство выглядит как набор ad hoc-трюков "а давайте построим такую хитровывернутую функцию". Иначе можно прогоняться за призраком неограниченное количество времени.

[svv]

cxzbsdhwert
Доказательство, схему которого Вы привели, сводит фальшивое разложение определителя матрицы $A$ к обычному разложению определителя другой матрицы $A'$ с двумя совпадающими строками. Вы это и сами понимаете. К этому моменту утверждение «определитель матрицы с двумя совпадающими строками равен нулю» уже доказано.

[cxzbsdhwert]

nnosipov в сообщении #1713825 писал(а):

cxzbsdhwert в сообщении #1713824 писал(а):

или дающееся на лекции доказательства исчерпывающее и нужно двигаться дальше

Или.

Всё-таки стоит за этим разумная идея, правда я её нашёл для определителя как такового, а не фальшивого разложения.

Фундамент идеи таков:
1. Пусть даны две пары чисел - $(a_1, b_1), (a_2,b_2)$.
2.1 Если $b_1$ содержится в $a_1$ в том же количестве, что и $b_2$ в $a_2$, т.е. $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}$ то $a_2$ будет содержаться в $a_1$ в том же количестве что и $b_2$ в $b_1$, т.е. $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}$.
Это требует (по крайней мере для меня) существенного осмысления, но тем не менее это так.
2.2 Если отношения $\dfrac{a_1}{b_1}$ и $\dfrac{a_2}{b_2}$ разные, то и отношения $\dfrac{a_1}{a_2}$ и $\dfrac{b_1}{b_2}$ разные.
3. Из вышеописанного, среди прочего следует, что строчный ранг матрицы равен столбцовому.

Тогда:
1. Рассмотрим для наглядности матрицу из вышеупомянутых пар

$$\mleft\begin{pmatrix} a_1& &b_1 \\ a_2& &b_2 \\ \end{pmatrix}$$

2. Пускай $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}$ (из чего следует $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}$).
3. Тогда, например, $a_2$ будучи представимым как $b_2$ в количестве равном количеству $b_2$ же в $a_2$, т.е. $a_2=b_2\dfrac{a_2}{b_2}$, по предположению 2 может быть представимо как $b_2$ в количестве равном количеству $b_1$ в $a_1$, т.е. $a_2=b_2\dfrac{a_1}{b_1}$. Умножив обе части равенства на $b_1$ получим $a_2b_1=b_2a_1$
4. Выражения $a_2b_1$ и $b_2a_1$ будут равны, то есть их разница $a_2b_1-b_2a_1$ будет равна нулю тогда и только тогда когда выполнено предположение пункта 2, что эквивалентно выполнению предположения о том, что строки матрицы линейно-зависимы, а в противном случае в виду отсутствия "паритета" равны они не будут, то есть их разница нулю не будет равна, что означает, что мы разумно задали функцию определителя.


Дальше эти соображения распространяются на случай матриц большего размера, по идее будет получатся $\dfrac{n!}{2}$ пар с разными знаками по модулю равных друг-другу (в случае вырожденности матрицы).
Это также объясняет почему в рамках каждого слагаемого, в двух строках не берутся элементы из одного столбца - ну просто потому что $a_1a_2\neq b_1b_2$ даже при линейной зависимости в общем случае - верно это будет только в частном случае л\з, с дополнительным условием $a_1=a_2$ и $b_1=b_2$. Но главное, что в общем случае предположения линейной зависимости такое равенство не соблюдается, поэтому мы в формулу определителя таких слагаемых и не добавляем.
Это также даёт понимание численного (а не качественного) содержания определителя - он показывает, если строки линейно независимы, то насколько количественно отличаются отношения пар элементов вдоль строк\вдоль столбцов.
Соображения конечно не объясняют почему определитель задан только на множествах квадратных матриц и наверное ещё другие нюансы, это конечно всё тоже важно, и вообще на таком этапе завершать размышления не стоит, потому что может оказаться что всё "не работает", но поскольку мы знаем что "работает", то мне достаточно на данный момент того, что я всё-таки нашёл разумность.

Полагаю, что и разумное доказательство фальшивого разложения, если оно, как и в случае с определителем есть, должно исходить из вышеописанной идеи.

[nnosipov]

cxzbsdhwert
А Вы кто (школьник, студент, ...)?

[cxzbsdhwert]

nnosipov в сообщении #1713980 писал(а):

cxzbsdhwert
А Вы кто (школьник, студент, ...)?

Можно считать студент