Группы обратимых элементов областей целостности

[KregSeptim]

Существует ли область целостности с группой обратимых, изоморфной $\mathbb{Z}$, если характеристика кольца не 2? А с $\mathbb{Z}^\mathbb{Z}$ в общем случае?
При попытках построить такие кольца мешается 2-кручение, которое отщепляется в кольцах характеристики не 2. Если же смотреть на характеристику 2, то удается построить область целостности с группой обратимых $\mathbb{Z}^{\bigoplus \mathbb{Z}}$ (и любые конечные степени) через полиномы Лорана, но не получается добраться до прямого произведения групп.

[dgwuqtj]

KregSeptim в сообщении #1713681 писал(а):

Существует ли область целостности с группой обратимых, изоморфной $\mathbb{Z}$, если характеристика кольца не 2?

Не существует, так как тогда $-1$ будет обратимым элементом порядка $2$.

KregSeptim в сообщении #1713681 писал(а):

А с $\mathbb{Z}^\mathbb{Z}$ в общем случае?

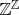
Возьмём вообще любую упорядоченную абелеву группу $A$ (ваша $\mathbb Z^{\mathbb Z}$ подходит, на ней существует линейный порядок, согласованный со сложением). И рассмотрим групповую алгебру

$$R = \mathbb F_2[A] = \{ \sum_{b \in B} [b] \mid B \subseteq A \text{ конечное} \}.$$

Это обобщение многочленов Лорана, т.к. $[b] + [b] = 0$ и $[b] [b'] = [b + b']$. Благодаря упорядоченности $A$ группа $R^*$ состоит из мономов, т.е. изоморфна $A$.

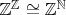
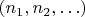
Порядок на $\mathbb Z^{\mathbb Z} \cong \mathbb Z^{\mathbb N}$ такой: элемент $(n_1, n_2, \ldots)$ положительный, если его первый ненулевой коэффициент положительный.