Корректность математической формулы и ИИ

[MGM]

Изначально была формула (весьма условная):
$F(u,v) = \left\{ {\begin{array}{*{20}{l}} {R(t,\theta (u,v)),}&{\quad v > 0\; \cup \;(v = 0\; \cap \;u > 0),} \\ {R(t,{\theta _0}),}&{\quad u = 0,\;v = 0,} \\ {{F^*}( - u, - v),}&{\quad v < 0\; \cup \;(v = 0\; \cap \;u < 0),} \end{array}} \right.$
where ${\theta _0} \in [0,\pi ).$
ИИ посоветовал следующее:
$F(u,v) = \left\{ {\begin{array}{*{20}{l}} {R(t,\theta (u,v)),}&{\quad v > 0\; \vee \;(v = 0\; \wedge \;u > 0),} \\ {R(t,{\theta _0}),}&{\quad u = 0,\;v = 0,} \\ {{F^*}( - u, - v),}&{\quad \text{else },} \end{array}} \right.$
Три вопроса:
а) насколько корректно использование $\wedge \vee $ в формулах по матанализу и некорректно $\cup \cap $?
б) Понятно ли что дополнение where ${\theta _0} \in [0,\pi ).$ означает что можно взять любое значение из интервала?
в) насколь безопасно обсуждать с DeepSeek доказательство своих собственных теорем, если потенциальное значение следствий таких теорем сам оцениваешь, как значительный прогресс?

[Mikhail_K]

MGM в сообщении #1713660 писал(а):

насколько корректно использование $\wedge \vee $ в формулах по матанализу и некорректно $\cup \cap $

Символы $\vee$ и $\wedge$ обозначают логические операции "ИЛИ" и "И" (дизъюнкцию и конъюнкцию), они ставятся между утверждениями. Символы $\cup$ и $\cap$ обозначают операции объединения и пересечения множеств, их можно применять к множествам. У Вас в правой части стоят утверждения. Например, $v>0$ - это утверждение (оно может быть верным или неверным в зависимости от $v$). Поэтому надо использовать символы $\wedge$ и $\vee$. Это так не только в мат.анализе, но и в любых разделах математики.

Upd. Немного ошибся, отредактировал пост.

[MGM]

Вопрос в) снимается, так как сам Deepseek настоятельно рекомендовал не делится с ним ничем ценным:

Цитата:

Если вы все же хотите использовать DeepSeek в исследовательской работе, но не раскрывать суть, следуйте этим правилам:

Избегайте конкретики: Обсуждайте общие концепции, методы или непрямые задачи, не раскрывая ключевых идей и точных формулировок.

Не загружайте файлы: Не прикрепляйте документы с доказательствами или кодом.

Настройте приватность: В веб-версии или приложении отключите функцию «Improve the model for everyone» / «Улучшим модель для всех», чтобы ваши диалоги не использовались для обучения.

Регулярно удаляйте чаты: Удаляйте историю диалогов в своем аккаунте, чтобы снизить риски в случае компрометации.

Хотя я сильно сомневаюсь, что в потоке из миллионов вопросов ИИ способен выделить особо ценную инфу. Если, конечно, это не мейнстрамная задача.

[Someone]

MGM в сообщении #1713665 писал(а):

Хотя я сильно сомневаюсь, что в потоке из миллионов вопросов ИИ способен выделить особо ценную инфу. Если, конечно, это не мейнстрамная задача.

Он не будет ничего выделять. Он просто будет использовать полученную от Вас информацию в своих ответах.

[MGM]

Mikhail_K в сообщении #1713664 писал(а):

MGM в сообщении #1713660 писал(а):

насколько корректно использование $\wedge \vee $ в формулах по матанализу и некорректно $\cup \cap $

Символы $\vee$ и $\wedge$ обозначают логические операции "ИЛИ" и "И" (дизъюнкцию и конъюнкцию), они ставятся между утверждениями. Символы $\cup$ и $\cap$ обозначают операции объединения и пересечения множеств, их можно применять к множествам. У Вас в правой части стоят утверждения. Например, $v>0$ - это утверждение (оно может быть верным или неверным в зависимости от $v$). Поэтому надо использовать символы $\wedge$ и $\vee$. Это так не только в мат.анализе, но и в любых разделах математики.

Первая формула (с поправкой на сказанное выше) противоречива, поскольку условие для первой строчки и условие для третьей строчки могут выполняться одновременно. Предложенная ИИ формула не противоречива, но не факт что соответствует тому что Вам нужно (мы тут не знаем, какая формула должна быть на самом деле). Вы может быть словами скажете, что должны означать условия в правой части формулы?

MGM в сообщении #1713660 писал(а):

Понятно ли что дополнение where ${\theta _0} \in [0,\pi ).$ означает что можно взять любое значение из интервала?

Не очень понятный вопрос, но пусть да. Только из полуинтервала.

MGM в сообщении #1713660 писал(а):

насколь безопасно обсуждать с DeepSeek доказательство своих собственных теорем, если потенциальное значение следствий таких теорем сам оцениваешь, как значительный прогресс?

Не бойтесь, не украдут, такие блуждания в трёх соснах как у Вас и не нужны никому.

Про три сосны - это, как раз то самое, на что я надеюсь. Ибо случайно наткнулся на решение, мимо которого ходили 50 лет. В том числе и я сам. Когда с опозданием в 30 лет занялся этой проблемой.
По поводу противоречивости - да, там ошибки, и область определения верхней полуплоскости плюс положительный луч может быть и не корректна в данной реализации. Но вопрос был о применении. По поводу обьединения множеств, в Топологии вполне себе области определения рассматриваются, как множества.

PS Отлаженный софт с результатами - мотивирует меня гораздо больше, чем верность или не верность доказательства. В том, что алгоритм работает, я полностю уверен, теперь надо бы это опубликовать - а это требует тщательной верификации для каждого чиха.

[Mikhail_K]

Someone в сообщении #1713667 писал(а):

Он не будет ничего выделять. Он просто будет использовать полученную от Вас информацию в своих ответах.

Сильно не факт - насколько я знаю, в современных ИИ нет автоматического дообучения на основе диалогов с пользователями. Здесь даже тема где-то об этом была.

На сайте Gemini сказано, что сотрудники могут просматривать беседы и как-то на основе этого дообучать ИИ, если пользователь явно это не запретит. Вероятно, что-то подобное, с явным разрешением пользователя или без него, имеет место и для других ИИ.

Сам я думаю, что использование ИИ в исследовательской работе безопасно (особенно учитывая, что я не гений, и думаю что ТС тоже не гений). Никому из разработчиков ИИ наши прорывы не нужны, никому не интересно их красть, а выделять из диалогов что-то ценное очень сложно и муторно. Опасность (для качества получаемой работы) тут может быть только в некритичном отношении к ответам ИИ.

-- 30.12.2025, 11:14 --

MGM в сообщении #1713668 писал(а):

По поводу обьединения множеств, в Топологии вполне себе области определения рассматриваются, как множества.

Ни в каком разделе математики нельзя путать символы $\vee$, $\wedge$ с символами $\cup$, $\cap$. У них просто разный смысл, хотя очень похожие свойства. Также ни в каком разделе математики нельзя путать множество с утверждением.

Конечно, области определения - это множества. $(0,+\infty)$ - это множество, оно может быть областью определения чего-нибудь.
$v>0$ - это утверждение (предикат), само по себе оно не область определения.

-- 30.12.2025, 11:16 --

MGM в сообщении #1713668 писал(а):

По поводу противоречивости - да, там ошибки, и область определения верхней полуплоскости плюс положительный луч может быть и не корректна в данной реализации.

Я отредактировал свой пост, противоречивости тут нет.

[MGM]

Mikhail_K в сообщении #1713669 писал(а):

Someone в сообщении #1713667 писал(а):

Он не будет ничего выделять. Он просто будет использовать полученную от Вас информацию в своих ответах.

Сильно не факт - насколько я знаю, в современных ИИ нет автоматического дообучения на основе диалогов с пользователями. Здесь даже тема где-то об этом была.

На сайте Gemini сказано, что сотрудники могут просматривать беседы и как-то на основе этого дообучать ИИ, если пользователь явно это не запретит. Вероятно, что-то подобное, с явным разрешением пользователя или без него, имеет место и для других ИИ.

Сам я думаю, что использование ИИ в исследовательской работе безопасно (особенно учитывая, что я не гений, и думаю что ТС тоже не гений). Никому из разработчиков ИИ наши прорывы не нужны, никому не интересно их красть, а выделять из диалогов что-то ценное очень сложно и муторно. Опасность (для качества получаемой работы) тут может быть только в некритичном отношении к ответам ИИ.

Выше мнение DeepSeek. Он дообучается. Говорит, что не советует, и у них были утечки, другое дело, что средней руки результаты (даже в топовых журналах) вряд ли так уж интересны вторым сторонам. Это надо, чтобы задачи ваши сильно совпадали с тем, кто использует вторичную информацию ИИ. В этом плане у меня все в порядке, так как есть устоявшееся мнение, что проблема решена окончательно к концу 80х.
Естественно я не гений, учитывая возраст и уровень публикаций, которы можно считать очень хорошим только в России. Однако решаю проблемы просто в свое удовльствие. Уже не связанные с тем, чем занимался в молодости, в том числе и в зарубежных университетах. И именно сейчас мне повезло (очень случайно, до этого я повторял все то, что народ погруженный в проблему делал лет 30 назад). Везение подтверждается реальными вычислительными результатами и отсутсвием публикаций с реализацией этой идеи. И тут-то и кроется подвох. Представте, что кто-то случайно доказал гипотезу Римана (почти невероятно, да и уровень моего везения все же не такой звездный), и во человек, утративший навыки формальных доказательств пытается улучшить читаемость и понятность этого доказательсва с ИИ. Вполне возможно, что есть мониторинговые жучки на такие знаковые проблемы. Поэтому буду консультироваться с некой опаской, не раскрывая

Mikhail_K в сообщении #1713669 писал(а):

Конечно, области определения - это множества. $(0,+\infty)$ - это множество, оно может быть областью определения чего-нибудь.
$v>0$ - это утверждение (предикат), само по себе оно не область определения.

-- 30.12.2025, 11:16 --

MGM в сообщении #1713668 писал(а):

По поводу противоречивости - да, там ошибки, и область определения верхней полуплоскости плюс положительный луч может быть и не корректна в данной реализации.

Я отредактировал свой пост, противоречивости тут нет.

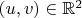
Это я понял, и за это спасибо и Вам и DeepSeek. Просто я опустил некоторые шаги. Сначала у меня было полное множество $\left( {u,v} \right) \in {\mathbb{R}^2}$ разделенное на два подмножества. И включение или невключение делало формулу более короткой и элегантной. Но потом появилась особая точка в нуле. И все поплыло.