Знак следования и равносильности в уравнении

[Girpodius]

Здравствуйте!
Будьте добры, подскажите, пожалуйста.
Уравнение, входящее в письменную часть ОГЭ (9 класс): $(5-2x)^4-13(5-2x)^2+36=0$
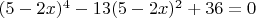
Моё решение имеет такой вид.
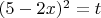
Пусть $(5-2x)^2=t$. Тогда

$t^2-13t+36=0$

$D=169-144=25$

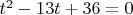
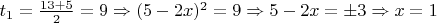
$t_1=\frac{13+5}{2}=9 \Rightarrow (5-2x)^2=9 \Rightarrow 5-2x=\pm3 \Rightarrow x=1$ или $x=4$

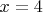
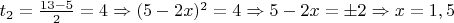
$t_2=\frac{13-5}{2}=4 \Rightarrow (5-2x)^2=4 \Rightarrow 5-2x=\pm2 \Rightarrow x=1,5$ или $x=4,5$

Ответ: $1; 1,5; 4; 4,5$

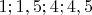
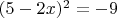
Я сознательно не пишу ограничение на $t$ ($t\geqslant0$), просто делаю обратную замену и если получится, что, например, $(5-2x)^2=-9$, то запишу, что $x$\in\varnothing$$.

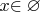
Вопрос в знаках следования. Мне тут сообщили, что использование знака следования здесь, дескать, некорректно. Нужно использовать знак равносильности, а для этого обязательно указывать ограничение $t\geqslant0$. Я понимаю, что можно, конечно, и через равносильность. Но мне кажется, что решение в данной записи через знак следования вполне корректно.

Возможно ли такое решение? Верно ли оно?

[dgwuqtj]

Girpodius в сообщении #1713571 писал(а):

Мне тут сообщили, что использование знака следования здесь, дескать, некорректно.

Если писать следствие в одну сторону, возникает вопрос, не могут ли появиться посторонние корни. Скажем, из $(5 - 2 x)^2 = -1$ формально следует $x = 0$ (из ложного утверждения следует всё, что угодно). Так что знаки равносильности в этом плане лучше. Ну или в конце руками проверяйте, что все найденные значения подходят.

Указывать ограничение $t \geq 0$ по идее не обязательно, но я к школьной математике отношения не имею, и как там принято, лучше ответят другие.

[EUgeneUS]

Girpodius
Фраза в заголовке темы: " Знак следования и равносильности в уравнении" крайне неудачная.
Знак следования или равносильности ставится не в уравнении, а между уравнениями.
Уравнения тут нужно рассматривать, как некие утверждения.

На мой взгляд знак следования тут вполне уместен.

dgwuqtj в сообщении #1713591 писал(а):

Скажем, из $(5 - 2 x)^2 = -1$ формально следует $x = 0$ (из ложного утверждения следует всё, что угодно).

Не будем доводить до абсурда, всё таки.
Если получили "ложное" при любых $x$ уравнение, то так и скажем: уравнение несовместно, корней нет.

dgwuqtj в сообщении #1713591 писал(а):

я к школьной математике отношения не имею, и как там принято, лучше ответят другие.

Плюс 1.

[Mihr]

EUgeneUS в сообщении #1713594 писал(а):

На мой взгляд знак следования тут вполне уместен.

Как сказать... Иногда - да, но, вообще-то, переходя к следствию, мы получаем решение другой задачи, отличной от исходной. И рискуем получить посторонние решения. Значит, нужно либо накладывать дополнительные условия, которые отсекут эти посторонние решения, либо в конце решения делать проверку с той же целью: отсеять посторонние решения, если они возникли. Если в процессе решения мы выполняли неравносильные преобразования (например, возводили уравнение в квадрат или другую чётную степень, отбрасывали знаки логарифмов или, скажем, арксинусов и т.д.), тогда проверка - не просто средство самоконтроля, а часть решения задачи. И если мы её не выполнили, то задача недорешена, даже если ответ случайно оказался точным. Это нужно хорошо понимать.

Girpodius в сообщении #1713571 писал(а):

Вопрос в знаках следования. Мне тут сообщили, что использование знака следования здесь, дескать, некорректно.

Покажите, пожалуйста, как именно Вы используете знаки следования. Пока в Вашем изложении решения задачи я каких-либо неравносильных преобразований не увидел.

Girpodius в сообщении #1713571 писал(а):

Возможно ли такое решение?

Я полагаю, да.

Girpodius в сообщении #1713571 писал(а):

Верно ли оно?

Не вполне:

Girpodius в сообщении #1713571 писал(а):

$t_2=\frac{13-5}{2}=4 \Rightarrow (5-2x)^2=4 \Rightarrow 5-2x=\pm2 \Rightarrow x=1,5$ или $x=4,5$

Ответ: $1; 1,5; 4; 4,5$

Правильный ответ: $1; 1,5; 3,5; 4$