Свойства определенного подмножества

[pan555]

Red_Herring в сообщении #1713713 писал(а):

pan555 в сообщении #1713528 писал(а):

Выбираем такое подмножестводробно-линейных преобразований, у которых расстояние между неподвижеыми точаами постоянно.

Означает ли ваш вопрос что "дано число $\rho>0$, и нужно найти все д.л.п. такие что расстояние между их неподвижными точками равно $\rho>0$? Ну тогда рассмотрим д.л.п., и его непосвижные точки заданы формулой $z_{1,2}$ ="одна фигная" $\pm$ "еще одна фигная" и расстояние между ними равно удвоенному модулю "другой фигни" . Пишем уравнение относительно четверки комплексных чисел.

(Оффтоп)

Если б у нас были устные экзамены и сохранялась оценка "E", то я бы использовал эту задачу, чтоб отделять "E" от "F". Увы, экзамены только письменные и оценка"E" ушла в небытие много десятилетий назад, вероятно, чтоб не травмировать тех, кто получил "F".

Сформулирую как можно точнее:
"дано число $\rho>0$, и нужно найти такое подмножесво д.л.п. ,что расстояние между неподвижными точками каждого д.л.п этого подмножества равно $\rho$ -конкретно одно значение.
Хотелось бы понять,может ли такое подмножество иметь какую либо знакомую мат.структуру ?

[yesterday]

Вот вы практически прямым текстом спрашиваете про $ISO(2)$, но зачем то настаиваете на дробно-линейных преобразованиях. Зачем?
Давайте начнём с того, откуда данная задача появилась

[pan555]

yesterday в сообщении #1713717 писал(а):

Вот вы практически прямым текстом спрашиваете про $ISO(2)$, но зачем то настаиваете на дробно-линейных преобразованиях. Зачем?
Давайте начнём с того, откуда данная задача появилась

В определенном смысле Вы правы.
Ибо в общем случае я такой вопрос бы задал потом и для преобразрваний Мебиуса -
- а они по факту дробно -квадротичные, и,как я понимаю, аналогичны $ISO(2)$.
Задача появилась из анализа линейных преобразований ,в которых ,по факту, неподвижная точка единственна. Более подробно показывать свои мат.фантазии смысла не вижу.

-- 31.12.2025, 11:45 --

yesterday в сообщении #1713717 писал(а):

Вот вы практически прямым текстом спрашиваете про $ISO(2)$, но зачем то настаиваете на дробно-линейных преобразованиях. Зачем?
Давайте начнём с того, откуда данная задача появилась

В определенном смысле Вы правы.
Ибо в общем случае я такой вопрос бы задал потом и для преобразрваний Мебиуса -
- а они по факту дробно -квадротичные, и,как я понимаю, аналогичны $ISO(2)$.
Задача появилась из анализа линейных преобразований ,в которых ,по факту, неподвижная точка единственна. Более подробно показывать свои мат.фантазии смысла не вижу.

[mihiv]

Всех с наступившим Новым Годом!

Д.л.п. $T(z)=\dfrac {z+a}{bz+c}$ соответствует матрица коэффициентов, зависящая от трех произвольных параметров $a,b,c$ (будем считать их действительными):

$$T=\left (\begin {array}{ccc}1&a\\b&c\end {array}\right )$$

Если наложить ограничение на расстояние между неподвижными точками: $|z_1-z_2|=R$, то один из параметров можно исключить, и матрица $T$ будет иметь, например, такой вид:

$$T=\left (\begin {array}{ccc}1&f(b,c)\\b&c\end {array}\right ), f(b,c)=\dfrac {R^2b^2-(c-1)^2}{4b}$$

dgwuqtj отметил, что множество д.л.п. с композицией в качестве бинарной операции не образуют группу. Рассмотрим другую операцию, обозначим ее $*:$

$$\left (\begin {array}{ccc}1&f(b_1,c_1)\\b_1&c_1\end {array}\right )*\left (\begin {array}{ccc}1&f(b_2,c_2)\\b_2&c_2\end {array}\right )=\left (\begin {array}{ccc}1&f(b_1b_2,c_1c_2)\\b_1b_2&c_1c_2\end {array}\right )$$

С использованием этой операции выполняются все аксиомы группы.

[pan555]

mihiv
Благодарю за совет!
Т.е. эта операция * - это произведение столбцов ?

[mihiv]

pan555
Нижняя строка матрицы "произведения" равна произведению нижних строк "сомножителей". В верхней строке первый элемент равен 1, а второй - это значение функции $f$, у которой аргументами взяты элементы нижней строки матрицы произведения.
Выражение для функции $f$ приведено для случая, когда параметры $a,b,c$ - действительные и $ab>0.$

[dgwuqtj]

mihiv в сообщении #1713893 писал(а):

Д.л.п. $T(z)=\dfrac {z+a}{bz+c}$

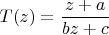
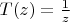
Не все дробно-линейные преобразования имеют такой вид. Например, $T(z) = \frac 1 z$ не такое, а у него неподвижные точки $\pm 1$.

mihiv в сообщении #1713893 писал(а):

один из параметров можно исключить, и матрица $T$ будет иметь, например, такой вид:

Это в вещественном случае. В комплексном исключить не получится, потому что требуемое множество размерности 5, а не 4.

pan555
Прежде чем думать про структуру группы, надо бы понять, что это за множество топологически. Вам же нужна именно топологическая группа (а то и группа Ли), а не абстрактное разрывное умножение. Топология зависит от того, считаете ли вы тождественное преобразование $\mathrm{id}$.

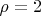
Если его не считать, то множество всех ваших преобразований раскладывается в произведение $\mathbb C$ и множества $X$ тех преобразований, у которых неподвижные точки — это диаметрально противоположные точки единичной окружности (для простоты пусть $\rho = 2$), так как любое преобразование получается из такого сопряжением при помощи единственного параллельного переноса. У $X$ есть двухлистное накрытие $\widetilde X$, если вместо преобразований рассматривать преобразования с пронумерованными неподвижными точками. 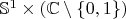Далее, $\widetilde X$ раскладывается как $\mathbb S^1 \times (\mathbb C \setminus \{ 0, 1 \})$, где второй сомножитель — это преобразования с неподвижными точками $1$ и $-1$ в фиксированном порядке. 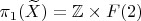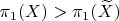Итого $\pi_1(\widetilde X) = \mathbb Z \times F(2)$ неабелева группа, и тем более $\pi_1(X) > \pi_1(\widetilde X)$ неабелева, а поэтому множество ваших преобразований не имеет структуры группы Ли. Зато множество является вещественно аналитическим многообразием.