Доказательство теор. Бэра (пересечение интервала с замкн.мн)

[cxzbsdhwert]

(Оффтоп)

Прошёлся по поиску, на форуме есть темы с обсуждением теорем Бэра похожих на ту, которая интересует меня, но терминология использующая в её формулировке и доказательстве от части мне не знакома, поэтому не уверен, что это та теорема. Если не так, то заранее извиняюсь за дублирование.

Теорема Бэра: Если замкнутое непустое множество $F$ представлено в виде объединения не более чем счётного (н.б.ч.с) набора замкнутых множеств $F_1,...,F_n$, то существует пересекающийся с $F$ интервал, пересечение которого принадлежит некоторому $F_n$.
Доказательство в оригинале тут

Я бы хотел обсудить несколько не до конца понятных моментов.

Лектор доказывал от обратного:
1. Пусть не существует интервала, пересекающегося с $F$, пересечение которого с $F_n$ принадлежит некоторому $F_n$.
2. Т.к. по условию набор $F_n$ н.б.ч.с., можем рассмотреть некоторый первый из них $F_1$.
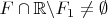
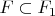
3. Пусть пересечение $F$ с дополнением $F_1$ до $\mathbb R$ непусто: $F\cap \mathbb R \backslash F_1 \neq \emptyset$. Иначе, предположение от противного ложно, так как тогда $F\subset F_1$ а значит любое пересечение с $F$ принадлежит и $F_1$.
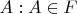
4. Поскольку пересечение дополнения с $F$ непусто, можем выбрать точку $A: A\in F$ и $A \in \mathbb R \backslash F_1$.
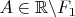
5. Дополнение к $F_1$ до $\mathbb R$ открыто, значит любая точка дополнения внутренняя (есть интервал, принадлежащий дополнению).
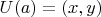
6. Тогда можно рассматривать некоторую окрестность $U(a)=(x,y)$, которая не пересекается с $F_1$, но пересекается с $F$ (может лежать в $F$, но необязательно). Эту окрестность можно произвольно сузить, не изменяя вышеперечисленных свойств. Пусть длина окрестности будет меньше 1. Эту окрестность можно симметрично сузить до отрезка.

7. Пусть $F$ также не равно $F_2$, следовательно, есть пересечение $F$ с дополнением $F_2$.
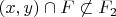
8. Пусть $(x,y)\cap F \not \subset F_2$, иначе предположение от обратного неверно.
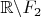
9. Тогда можно выбрать точку $a_2$ из $\mathbb R \backslash F_2$, так чтобы она была и точкой $(x,y)\cap F$.
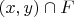
10. Поскольку $a_2$ точка открытого множества - дополнения $F_2$, то она входит с некоторой окрестностью, не пересекающейся с $F_2$.
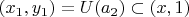
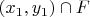
11. Рассмотрим новый интервал $(x_1,y_1)=U(a_2)\subset (x,1)$, $(x_1,y_1)\cap F$, т.к. содержит $a_2$ из $F$. Пусть длина этого интверала в два раза меньше длины $(x,y)$. Этот интервал также можно рассматривать как отрезок с такими же концами.

12. Пусть $F_3\neq F$, $(x_1,y_1)\cap F \not \subset F_3$.
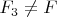
13. $\exists a_3 \in F \backslash F_3 : a_3 \in (x_1, y_1) \cap F$.
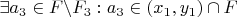
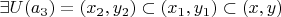
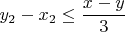
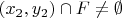
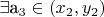
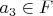
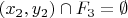
14. $\exists U(a_3)=(x_2,y_2) \subset (x_1, y_1) \subset (x,y)$ и $y_2-x_2 \leq \dfrac{x-y}{3}$ и $(x_2,y_2)\cap F \neq \emptyset$, т.к. \exists $a_3 \in (x_2,y_2)$ и $a_3 \in F$ и $(x_2,y_2) \cap F_3 = \emptyset$. Существует также и отрезок $[x_2,y_2]$, удовлетворяющий перечисленным свойствам.

15. Продолжая, получится н.б.ч.с система вложенных отрезков, пересечение которых, по принципу полноты Кантора непусто, в частности равно точке, если набор отрезков счётен и их длины стремятся к нулю.
16. Делается вывод о том, что $[x_n,y_n]$ не пересекается с $F_n$.
17. Тогда есть как минимум точка из пересечения всех отрезков, которая не пересекается ни с одним из $F_n$, но принадлежит $F$.
18. Поскольку по условию $F$ состоит только из $F_n$ то точка(точки) одновременно в $F$ и не в $F$ - противоречие.

Вопросы:
1. А если изначально пересечение интервала с $F$ состоит из одной точки или конечного (наверное даже счётного подойдёт) множества одноточечных множеств?
$F$ - замкнуто, одноточечное множество - замкнуто. н.б.ч.с объединение замкнутых множеств замкнуто, следовательно $F$ может быть н.б.ч.с. объединением точек.
Тогда, сужая интервалы под каждый $F_n$, так чтобы с ним не пересекаться, найдётся такой $F_n$, точка которого является единственной точкой системы отрезков (интервалов), в части, пересекающейся с $F$.
И тогда уменьшенный отрезок (интервал) не будет пересекаться вообще со всем $F$ и на следующей итерации нельзя будет взять новую точку из пересечения $F$, так чтобы она была и в новом интервале, ну и противоречия в итоге никакого не возникнет.
2. Если $F_n$ окажется принадлежащим, на некотором этапе, пересечению интервала с $F$, и тогда пересечение интервала с $F$ без такого $F_n$ приведёт к разбиению интервала на непересекающиеся интервалы, то нужно будет просто продолжить итерации на каждый интервал по отдельности? Или достаточно продолжать рассматривать только один?

[mihaild]

cxzbsdhwert в сообщении #1713331 писал(а):

А если изначально пересечение интервала с $F$ состоит из одной точки

Тогда эта точка принадлежит какому-то $F_i$, и значит пересечение нашего интервала с $F$ - подмножество $F_i$.

cxzbsdhwert в сообщении #1713331 писал(а):

н.б.ч.с объединение замкнутых множеств замкнуто

Это неправда. Существуют незамкнутые счетные множества.

cxzbsdhwert в сообщении #1713331 писал(а):

Если $F_n$ окажется принадлежащим, на некотором этапе, пересечению интервала с $F$, и тогда пересечение интервала с $F$ без такого $F_n$ приведёт к разбиению интервала на непересекающиеся интервалы, то нужно будет просто продолжить итерации на каждый интервал по отдельности?

А какая вообще разница? Нужно будет взять какой-нибудь один короткий интервал, пересекающийся с $F$, но не с $F_n$.

[cxzbsdhwert]

mihaild в сообщении #1713334 писал(а):

Тогда эта точка принадлежит какому-то $F_i$, и значит пересечение нашего интервала с $F$ - подмножество $F_i$.

Ну да

mihaild в сообщении #1713334 писал(а):

Это неправда. Существуют незамкнутые счетные множества.

Да, была теорема о том, что замкнутое множество есть объединение конечного, а не н.б.ч.с. набора. Только не понял, как существование незамкнутых счетных множеств исключает существование замкнутых.
$\mathbb N$ же замкнуто? Вы наверное имели в виду под объединением счетного числа замкнутых множеств рациональный интервал?

У $\mathbb N$ нет предельных точек, граничные точки оно все свои содержит. Дополнение к $\mathbb N$ это объединение счетного набора интервалов: $(-\infty, 1)\cup (1,2) \cup (2,3) \cup ...$, все они открытые множества, а у нас была теорема, что всякое объединение открытых множеств открыто, значит дополнение к $\mathbb N$ открыто, а значит, $\mathbb N$ замкнуто по определению, с учётом всех обстоятельств.

[mihaild]

cxzbsdhwert в сообщении #1713335 писал(а):

Только не понял, как существование незамкнутых счетных множеств исключает существование замкнутых.

Вы написали

cxzbsdhwert в сообщении #1713331 писал(а):

н.б.ч.с объединение замкнутых множеств замкнуто

Это обычно означает "для любого не более чем счетного семейства замкнутых множеств, их объединение замкнуто". Что неправда.
Конечно, бывают и счетные, и даже континуальные семейства замкнутых множеств, объединение которых замкнуто. Но это другой вопрос.

[cxzbsdhwert]

mihaild в сообщении #1713337 писал(а):

Это обычно означает "для любого не более чем счетного семейства замкнутых множеств, их объединение замкнуто". Что неправда.

Да, согласен

[skobar]

(Оффтоп)

Вряд ли это поможет ТС, но все же напишу. IMHO если не знать контекста общей теории, то разобраться в той форме, как это здесь изложено, практически невозможно. Формально после нудного прочтения можно вроде как все понять, но понимания по сути это едва ли прибавит.

Это не теорема Бэра, это частный случай следствия из теоремы Бэра. Настоящая теорема Бэра говорит, что полное метрическое пространство, как и локально компактное хаусдорфово пространство является пространством Бэра. В качестве следствия из неё сразу же выводится, что полное метрическое пространство является множеством второй категории (в себе). Далее любое (непустое) замкнутое подмножество $F$ множества всех вещественных чисел $\mathbb{R}$ является полным метрическим пространством в индуцированной топологии как замкнутое подмножество полного пространства $\mathbb{R}$. Поэтому, по следствию из теоремы Бэра $F$ будет множеством второй категории (в индуцированной топологии), откуда сразу следует, что если $F$ представлено в виде (не более чем) счетного объединения замкнутых множеств, то хотя бы одно из них будет иметь непустую внутренность. Именно этот частный случай следствия из теоремы Бэра и рассматривается в теме.

IMHO в контексте общей теории все становится понятнее и "становится по своим местам", чем если рассматривать только данный частный случай, из которого совершенно непонятно, откуда берутся такие странные, кажущиеся искусственными непонятные формулировки.

[Mikhail_K]

skobar в сообщении #1713342 писал(а):

Вряд ли это поможет ТС, но все же напишу. IMHO если не знать контекста общей теории, то разобраться в той форме, как это здесь изложено, практически невозможно. Формально после нудного прочтения можно вроде как все понять, но понимания по сути это едва ли прибавит.

Поддерживаю.