Задача о минимуме комплексной функции

[pavelyoung]

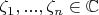
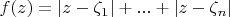
Задача: даны комплексные числа $\zeta_{1}, ..., \zeta_{n} \in \mathbb{C}$. Найти такое число $z \in \mathbb{C}$ (или множество всех таких чисел), что $f(z) = |z-\zeta_1|+...+|z-\zeta_n| - минимально.

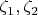
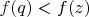
Я решил решить геометрически. Сначала расскажу про мое решение частного случая: при $n=2$. Проведем прямую $l$, проходящую через точки $\zeta_1, \zeta_2$. Понятно, что z, которое мы хотим найти, лежит на прямой l. (Иначе, мы бы могли провести перпендикуляр к прямой l, проходящий через z, и основание этого перпендикуляра (назовем q), будет лучше: $f(q) < f(z)$). Теперь попробуем примерно найти такое z. Пускай $\varepsilon > 0$ - очень малое число, которое мы устремим к нулю в будущем. Прочертим прямую m, параллельную l, и находящуюся на расстоянии $\varepsilon$ от l. 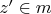Тогда попробуем найти точку $z' \in m$, с минимальным значением f. И эта задача уже имеет известное и красивое решение: найдем точку $\psi$, которую можно получить симметрично отразив $\zeta_2$ относительно m. Так как наша точка z' лежит на m, то сумма расстояний от z' до $\zeta_1$ и $\zeta_2$, будет такой же, что и сумма расстояний до $\zeta_1$ и $\psi$. 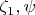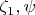Так как точки $\zeta_1, \psi$ лежат по разные стороны от прямой m, то отрезок, границы которого - $\zeta_1, \psi$ будет пересекать m. И место пересечения - будет минимальным z'. И при $\varepsilon \rightarrow 0$, выходит $z' \rightarrow \dfrac{\zeta_1 + \zeta_2}{2}$. 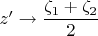Это и есть ответ на вопрос.

Вот в общем случае точки могут и не лежать на одной прямой. И вопрос уже сводится к такому:
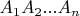
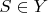
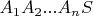
Задан многоугольник $A_1 A_2 ... A_n$ на плоскости X с заданными вершинами, и плоскость Y, параллельную с X. при этом находясь на расстоянии $\varepsilon$ с ней. Как найти точку $S \in Y$, так чтобы периметр пирамиды $A_1 A_2 ... A_n S$ с основанием $A_1 ... A_n$ был минимален?

[mihaild]

pavelyoung в сообщении #1713308 писал(а):

Это и есть ответ на вопрос.

Возьмем $\zeta_1 = 0$, $\zeta_2 = 2$. Разве точка $z = 1$ - единственный минимиум $f$?

А Вы уверены, что в условии именно модули, а не квадраты модулей? Для суммы модулей решения в замкнутой форме не существует.

[TOTAL]

pavelyoung в сообщении #1713308 писал(а):

$ \dfrac{\zeta_1 + \zeta_2}{2}$. Это и есть ответ на вопрос.

$ \dfrac{2\zeta_1 + \zeta_2}{3}$
А вот такой ответ подойдёт?

[pavelyoung]

Я неимоверно затупил. Любая точка, лежащая на отрезке $\zeta_1, \zeta_2$ будет решением. Так что $\forall \ t \in [0, 1]$ решением будет $t\zeta_1 + (1-t)\zeta_2$

[dgwuqtj]

Если точки три и они не лежат на одной прямой, то ответом будет точка Ферма (если в треугольнике, образованном точками, есть вершина с углом $\geq 120^\circ$, то она и будет точкой Ферма).

И если все точки лежат на одной прямой, решение можно легко описать в общем виде.

[serg_yy]

Для трёх точек вам сказали ответ.
Для четырёх точек (где никакие три не лежат на одной прямой) ответом будет точка пересечения диагоналей соответствующего четырёхугольника.
В общем случае нет "хорошего" решения, решают обычно численными методами.

[dgwuqtj]

serg_yy в сообщении #1713326 писал(а):

Для четырёх точек (где никакие три не лежат на одной прямой) ответом будет точка пересечения диагоналей соответствующего четырёхугольника.

Это если они в выпуклом положении. А иначе эта та точка из заданных, которая строго внутри выпуклой оболочки.

[mihiv]

Пусть минимум $f(z)$ достигается при $z=z_0$. Для произвольного $z$ выполняется неравенство

$$f(z)\leqslant \sqrt {n\sum _{k=1}^n|z-\zeta _k|^2}\eqno (1)$$

Правая часть неравенства $(1)$ минимальна при $z=z_c=\dfrac {\zeta _1+\dots +\zeta _n}{n}$. Отсюда получается верхняя оценка

$$f(z_0)\leqslant f(z_c)\leqslant \sqrt {n\sum _{k=1}^n|z_c-\zeta _k|^2}$$